今回は、「対数/logの基本的な計算」についての説明です。
1.初めに
実際に社会に出てから使うかと言うと怪しいところですが、数学を勉強する上で対数であるlogの計算問題は多々出てきます。
今回は、そんなlogの計算をする上で知っておくべき基本的な性質や計算法則について簡単にまとめてみました。
『対数とかlogって何?』という状態の方は先に以下の記事に目を通してください。

2.logの基本的な性質
まずはlogの基本中の基本の考え方から入っていきます。
logの持つ基本的な性質は以下の2つです。
①底=真数なら対数は1になる。
②真数が乗数になっているとlogの外に出すことができる。
①底=真数なら対数は1になる。
x=log22という式があった場合、x=1ですよね?
指数の形に直すと2x=2だから当然の結果です。
この関係を言葉で表しただけです。
底とか真数という用語が出てくるからなんか難しそうな言い回しになっているだけです。
②真数が乗数になっているとlogの外に出すことができる。
x=log24という式があった場合、x=2ですよね?
指数の形に直すと2x=4だからこれまた当然の結果です。
つまり、x=log24=log222=2log22と式を変形することができます。
ここに「①底=真数なら対数は1になる。」を適用することで、x=2と計算することが可能です。
ちなみに、真数が分数だったり平方根になってたりしてもこの関係は成り立ちます。
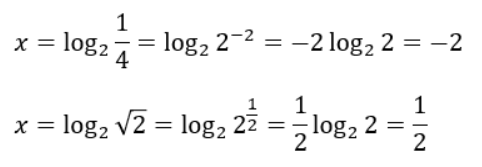
3.logの足し算・引き算・掛け算・割り算
対数同士の足し算/引き算の公式は以下の通りです。
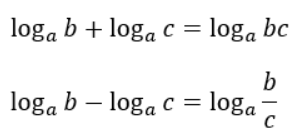
左辺と右辺を反対にすれば対数同士の掛け算/割り算の公式にもなります。
見た目が大分ややこしくなってきましたが、よくよく考えると当たり前の関係になっています。
対数同士の足し算を例として考えてみます。
そもそも、対数を足し合わせるってどういうことでしょうか?
3+4=7ですよね。
これを対数に当て嵌めると、3(底の3乗)+4(底の4乗)=7(底の7乗)となるわけです。
底が何乗なのか、その乗数が大きくなるわけです。
例えば、log28+log216=log223+log224=3log22+4log22=7log22=7となります。
この関係を見てわかる通り、ここで言う“7”とは底である2の7乗(log227)になるということを指しています。
つまり、真数は23×24になっているんですよ。
この関係をまとめると最初の関係式のようになるわけです。
同様に引き算についても考えてみると、真数の割り算になるのです。
注意すべき点は、底が同じじゃないと計算ができないという点ですね。
あくまで底が同じだからこそ成り立つということを忘れないようにしましょう。
4.底の変換公式
主だった関係式について説明してきましたが、一部特殊な法則があります。
それは、以下のような関係です。
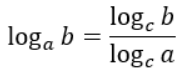
この公式のことを底の変換公式と呼びます。
ある対数があった時、任意で決めた底を持つ対数に変換できる公式です。
logの計算をする際に底がバラバラだった場合に活用します。
どうしてこの関係が成り立つのかの証明は以下の通りです。
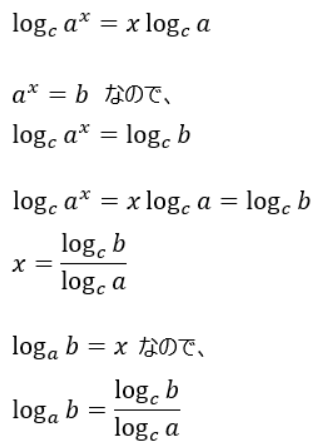
また、この底の変換公式に対して底の変換公式を当て嵌めて変形していくと、次のような関係式も導き出せます。
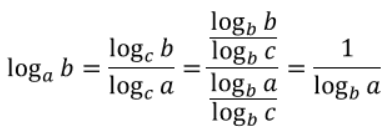
形としては比較的覚えやすいですね。
言葉で表すと、「ある対数は、底と真数を入れ替えた対数の逆数に等しい」ということになります。
うん、わかりづらいね。
5.例題
式を見ただけでは記憶に定着しないので、例題で実際に使用してみましょう。
logの引き算で底が同じなので、真数同士で割り算をすることは可能です。
log2(6÷3)=log22=1
底がバラバラなので、底の変換公式で底を揃えます。
今回は「ある対数は、底と真数を入れ替えた対数の逆数に等しい」の関係式の方を使ってみます。
log29×log32=2log23×(1/log23)=2log23÷log23=2
普通に変換公式を使っても計算可能なので、試しにやってみるのも良いと思います。
以上、「対数/logの基本的な計算」についての説明でした。



