【数学の雑学】 実数・虚数・自然数などの定義と意味の違いをわかりやすく解説！

今回は、「実数・虚数・自然数などの定義と意味の違い」についての説明です。

１．初めに

学校で習った数字には様々な種類があります。
例えば、以下のような“○○数”という用語は聞き覚えがあるのではないでしょうか？

ただ、どれが何を示しているのかを明確に説明できる人は少ないと思うんですよね。
日常生活でそこまで意識する必要が無いので、時間経過でみんな忘れていくんですよ。
似たような数字もありますしね。

今回は、そんな数字の定義や意味について噛み砕いて簡単にまとめていこうと思います。

２．実数とは？

実数[real number]とは、数直線上に存在するすべての数だと言われています。
知っている身からするとこの説明で言いたいことはわかるのですが、知らない人にこんな説明しても混乱するだけに決まっているんですよね。
数直線ってなんだよ、と。

この説明で理解するには図が必要です。

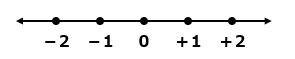
図1には0・正の数・負の数を表示してあります。
これが数直線です。
数を増やす/減らすことで一直線に繋がる数字は全部実数なんです。

なので、1と2の間にある1.5などの小数も実数ですし、平方根を使用した√2(約1.41)なども実数となります。
要するに、その名が示す通り、実際に存在する数が実数なのです。

後述する虚数以外のすべての数が実数に当たります。
その為、数字というものを大きく分類すると、実数か虚数のどちらかになります。
日常生活で使う数字は全部実数だと思えば問題無いです。

この実数は、有理数か無理数のどちらかに分類されます。

３．虚数とは？

虚数[imaginary number]とは、実際には存在しない2乗したら符号がマイナスになる数のことです。
2乗…べき乗の考え方は別途まとめるので、ここでは同じ数を2回掛けることだと思ってください。

数学の世界では“i”、電気の世界では“j”と表現されます。
要するに、「i×i=－1」になるのです。
つまり、“i”は√(－1)のことです。
この“i”のことを虚数単位と呼びます。

虚数単位があると計算で何かと便利なので定義されています。

図1の横方向が実数でしたよね？
この図の縦方向の世界が虚数に当たります。

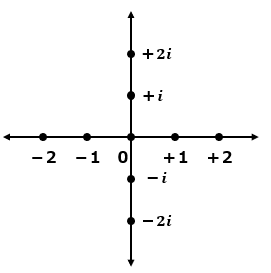
そんな数存在するわけがないでしょう？
だから[imaginary(想像上の・仮想的な)]な数なのです。

虚数を詳しく理解するには、まずは複素数から理解する必要があります。

４．複素数とは？

複素数[complex number]とは、2つの実数a,bと虚数単位iを用いてa+biと表現できる数のことです。
aを実部、bを虚部と呼びます。
多分実数部分、虚数部分を縮めて呼んでいるのではないかと思います。

例えば、1+2iという複素数が存在したら、1が実数で2iが虚数になります。
これに関してはそういう概念であると覚えてもらうしかないです。

複素数のイメージは座標表示です。
図2で示した横軸実数、縦軸虚数の平面モデルのことを複素数平面と呼びます。
複素数平面上に1+2iをプロットすると図3の位置になりますよね？

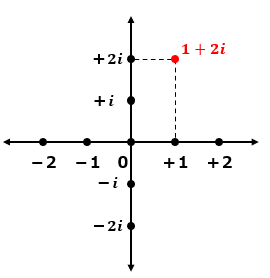
ここで、横軸を東西、縦軸を南北、単位を[m]に当て嵌めたとします。
すると、東に1m、北に2mの位置にいることがわかります。
仮に実数という概念しか存在しなかった場合、北にどれだけ進んでいるかは表せませんよね？
そこで虚数という概念を組み込んだ表現方法が複素数なのです。

複素数はそういうものだとして、何故2乗したら符号がマイナスになる虚数単位を使っているのかが謎ですよね？
これにはちゃんと意味があります。

1+2iの地点を点Aとして、点Aの複素数に虚数単位iをかけると、以下のようになります。

(1+2i)×i=i+2i²=i+2×(－1)=－2+i

この点を複素数平面上にプロットすると点Bの位置に移動します。

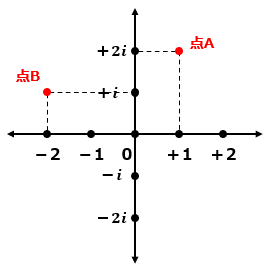
ここで、点Aと点Bの位置関係に注目してください。
0+0iを原点として、反時計回りに90度回転しただけだとわかりますでしょうか？

同様に点Bにiをかけた点C、点Cにiをかけた点Dをプロットすると、以下のようになります。

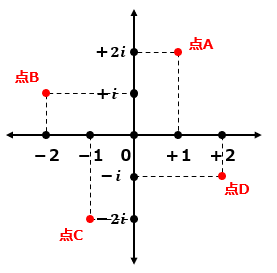
このように、虚数単位iをかけると、複素数平面上で反時計回りに90度ずつ座標が移動していくのです。
その結果、虚数単位iを4回かけると元の座標に戻ってきます。
この性質が何かと便利なので虚数単位が使用されています。

５．有理数とは？

有理数[rational number]とは、整数の比で表すことのできる数のことです。
簡単に言えば、分数で表現できる数のことです。
ただし、分母は0以外の整数という条件があります。

例えば、1は1/1と表現できますよね？なので有理数です。
－0.5は分数に直すと－1/2となるので、これも有理数です。
割り切れない1/3(0.333…)なんかも有理数です。

有理数は整数と分数(整数以外の有理数)に分類されます。
先程の例に当て嵌めると、1/1が整数で、－0.5と1/3は分数(小数)という扱いになりますからね。

実数の分類はこの有理数と後述の無理数に分かれます。

６．無理数とは？

無理数[irrational number]とは、整数の比で表すことのできない数のことです。
簡単に言えば、分数で表現できない数のことです。
有理数の逆ですね。

例えば、円周率πって分数で表現できますか？
円周率は年代によって3と習っていたり3.14と習っていたりと差はあるかもしれませんが、アレは本当は3.14159…と無限に続いていきます。
なので、分数で表すことは不可能です。

他にも平方根を使用した√2などの数字も無理数になります。
総じて、循環しない(規則性の無い)無限に続く小数になるものは無理数に当たります。
ただし、「不規則な」という注釈が付きます。
1/3(0.333…)のような同じ数が循環する循環小数は有理数だからです。

実数の分類はこの無理数と前述の有理数に分かれます。

７．整数とは？

整数[integer,whole number]とは、0及び0から1を足したり引いたりした数の事です。
－2,－1,0,＋1,＋2とかですね。
符号がプラスなら正の整数、マイナスなら負の整数と呼ばれます。

0に対して1ずつ刻んでいく数字を指しているため、合間に存在する－0.5などの小数、1/3などの分数は整数に含まれません。

形が整っている数と覚えると良さそうですね。

８．自然数とは？

自然数[natural  number]とは、個数もしくは順番を表す数のことです。
簡単に言えば、正の整数のことです。
ただし、0は含みません。

例えば、箱の中にあるみかんの数を数えておくように頼まれたとします。
そんな時、まず0から数えますか？
普通1から順番に『1個、2個…』と数えていきますよね？
このように、自然に数える数を自然数と呼ぶのです。
だから0は含まないんです。

ただ、これは高校数学までで習う場合です。
大学以降になると、0以上の正の整数だと定義されていることがあります。
違いは、0を含んで考えるか含まないで考えるかという定義の違いしかないです。
なので、その時々の定義次第で0を含むかどうかは変わってきます。
どちらかが間違っているわけではありません。

0を含まない場合は正整数、0を含む場合は非負整数という呼び名があるので、紛らわしい場合はこの呼び名を使うのが無難です。

９．素数とは？

素数[prime number]とは、1よりも大きい自然数の中で、1とその数自身でしか割りきれない数のことです。
要するに、2,3,5,7,11などの自然数のことです。

素数には実は判断方法があります。

例えば、100までの数字なら、以下に当て嵌まるもの以外が素数になります。

ちなみに、100より大きな数になると、7以上の素数である11や13などについても確認する必要が出てきます。
まあ、そこまで確認しなければならない状況に遭遇することは無いとは思いますが。

１０．イメージ図

ここで紹介した数字の関係をイメージしやすいように図にまとめました。
各説明と照らし合わせてみてください。

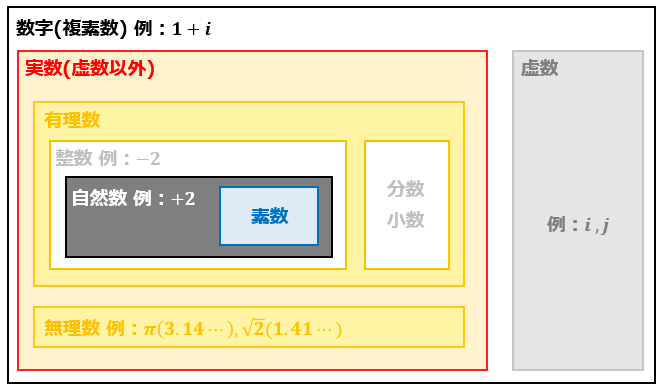
以上、「実数・虚数・自然数などの定義と意味の違い」についての説明でした。

---