今回は、「和積の公式」についての説明です。
1.和積の公式とは?
三角関数の和積の公式とは、左辺が和になっていて、右辺が積になっている公式を指します。
つまり、sinα+sinβ、sinα-sinβ、cosα+cosβ、cosα-cosβの公式です。
sinα+cosβなどは調べても公式が出てこなかったですが、実際のところないわけでもなさそうな気もしますがどうなんでしょうね?
とりあえずよく知られている4つの公式について考えていきます。
「積和の公式」の説明でも述べましたが、この辺から公式の見た目がゴツゴツしてきて単純に覚えるのが困難になってきますので、しっかりと導き方を理解して記憶に定着させるように頑張りましょう。
やり方さえわかってしまえばすぐに導き出せますからね。
肝心の和積の公式は以下の4式となります。
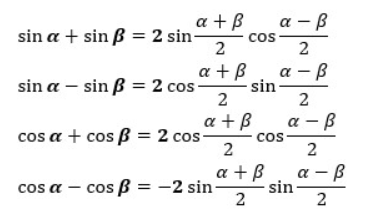
どうしてこうなるかは次の項から証明していきますね。
2.sinα+sinβの証明
まずはsinα+sinβの証明から始めます。
ここでは、積和の公式であるsinαcosβ={sin(α+β)+sin(α-β)}/2を使用していきます。
使用すると言っても、ちょっと工夫して足し算するだけなんですけどね。
この関係式において、α=(A+B)/2、β=(A-B)/2を代入してみます。
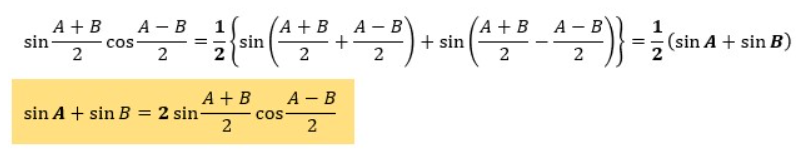
はい、証明完了です。
3.sinα-sinβの証明
次はsinα-sinβの証明です。
ここでは、積和の公式であるsinαcosβ={sin(α+β)+sin(α-β)}/2を使用していきます。
※ この時点でわかったかもしれませんが、残りの証明も積和の公式に何かしらを代入して計算するだけです。
この関係式において、α=(A-B)/2、β=(A+B)/2を代入してみます。
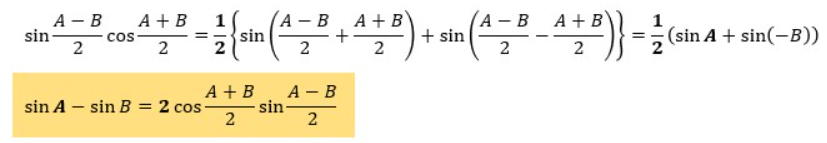
ちなみに、sin(-A)=-sinAです。
x軸y軸上に図示して見ればわかりますが、sin(-A)はsinAをx軸反転させたものとなります。
つまり、y方向の符号が反転するだけです。
4.cosα+cosβの証明
次はcosα+cosβの証明です。
ここでは、積和の公式であるcosαcosβ={cos(α+β)+cos(α-β)}/2を使用していきます。
この関係式において、α=(A+B)/2、β=(A-B)/2を代入してみます。
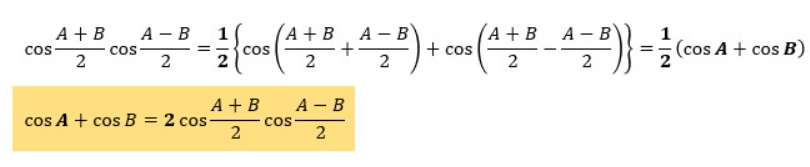
5.cosα-cosβの証明
最後にcosα-cosβの証明です。
ここでは、積和の公式であるsinαsinβ=-{cos(α+β)-cos(α-β)}/2を使用していきます。
この関係式において、α=(A+B)/2、β=(A-B)/2を代入してみます。
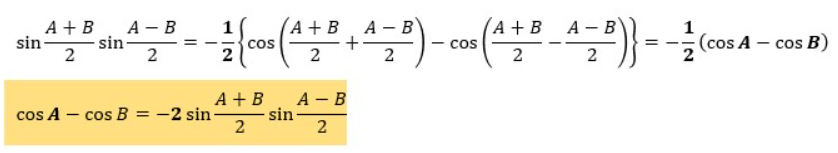
以上です。
計算は簡単なのですが、証明の為に積和の公式が必要で、積和の公式の証明には加法定理が必要になるので流石にわかりづらくなってきます。
使用頻度はあまり高くないので、解法を頭の片隅に置いといてなんとか引っ張り出せるようになっておくと学校のテストで役に立つかもしれないですよ?
社会に出たら使う機会なんてそうはないですけどね。
以上、「和積の公式」についての説明でした。



