今回は、「加法定理」についての説明です。
1.加法定理とは?
三角関数には様々な公式・定理が存在します。
この記事では、加法定理について説明していきます。
加法定理は、加法=足し算に関する定理です。
『sinα+sinβとかの関係式?』と思うかもしれませんが違います。
sin(α+β)の関係式です。
学校で『sin(α+β)=sinαcosβ+cosαsinβだから、右辺がsin・cos・cos・sinの順番で“咲いた コスモス コスモス 咲いた”と覚えよう!』とか習った記憶がありますが、この覚え方だと左辺との関連性が全くないから寧ろ混乱した覚えがあります。
私はcosは左辺と右辺の符号が反転するという点だけ覚えて、順番は“コスモス コスモス コスモス”と覚えたりしていました。
もうコスモスである必要がないですね(笑)
tanは普通に覚えづらいですが、最悪tanθ=sinθ÷cosθの関係から導き出せますので覚える必要性はあまりないです。
一応、“イチマイナスタンタン分のタンプラタン(1-tantan分のtan+tan)”というリズムで覚えるようには習いましたが…この辺までくると意味がわかりませんね。
肝心の加法定理は以下の3式となります。
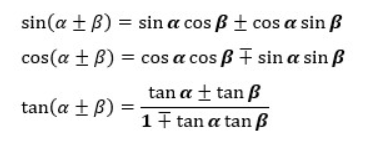
どうしてこうなるかは次の項から証明していきますね。
2.加法定理の証明 ~cos(α+β)~
まずはcos(α+β)の公式の証明からです。
なんでsin(α+β)からじゃないかと言うと、sin(α+β)の公式の証明にcos(α+β)を使うと早いからです。
大人の事情というヤツです。
図1のように単位円上の4点をそれぞれ繋いで△OABと△OCDを描きます。
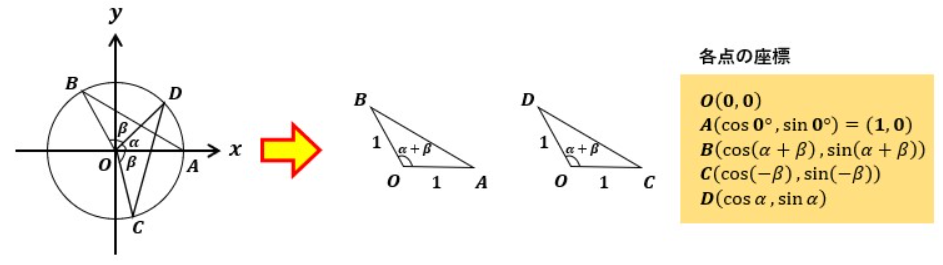
△OABと△OCDは2辺の長さが等しく、その間の角がどちらもα+βになっているので合同(同じ三角形)と言えます。
つまり、AB2=CD2になります。
AB2とCD2を座標から計算して照らし合わせてみると、以下のようになります。
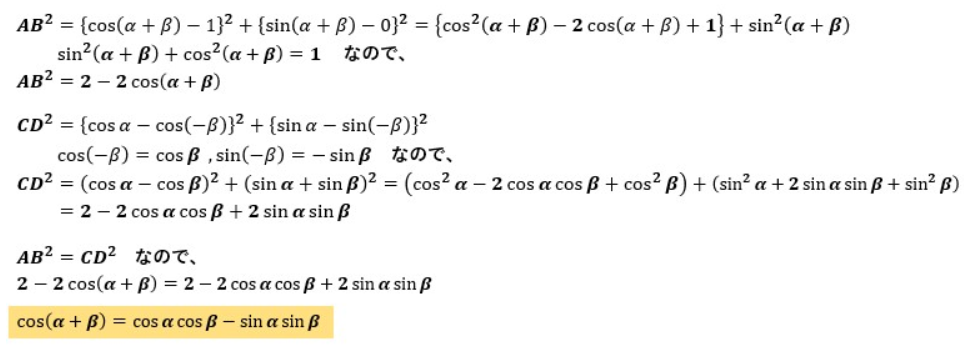
これでcos(α+β)=cosαcosβ-sinαsinβの公式の証明ができました。
ちなみに、角度がα-βになるような三角形を単位円上の点から作り出して同様に考えていけば、cos(α-β)=cosαcosβ+sinαsinβの関係式も証明可能です。
やることは同じなので省きますけど。
3.加法定理の証明 ~sin(α+β)~
次はsin(α+β)の公式の証明です。
sin(θ+90°)=cosθとcos(θ+90°)=-sinθという公式と、先程照明したcos(α+β)の関係式を利用して導いていきます。
sin(θ+90°)=cosθとcos(θ+90°)=-sinθについては三角関数と象限の関係を説明した際に証明を済ませていますので、気になる方はそちらもご覧ください。

まず、sinθ=-cos(θ+90°)なので、θにα+βを代入してsin(α+β)=-cos(α+β+90°)にします。
ここで、右辺にcos(α+β)=cosαcosβ-sinαsinβの公式を適用すると、
sin(α+β)=-cos(α+(β+90°))=-(cosαcos(β+90°))-sinαsin(β+90°))
となります。
sin(θ+90°)=cosθ、cos(θ+90°)=-sinθなので、
sin(α+β)=-(-cosαsinβ-sinαcosβ)=sinαcosβ+cosαsinβです。
これで証明完了です。
4.加法定理の証明 ~tan(α+β)~
最後にtan(α+β)の公式の証明です。
sin(α+β)とcos(α+β)の公式を代入して整理していくだけですけどね。
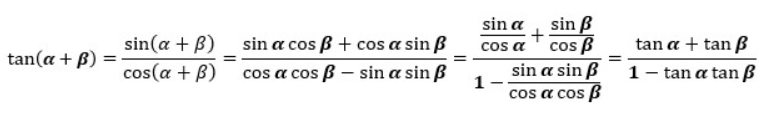
以上、「加法定理」についての説明でした。



