今回は、「半角の公式」についての説明です。
1.半角の公式とは?
三角関数の半角の公式とは、sin2(α/2)のように角度が1/2倍になっている場合の公式を指します。
形がスッキリするのが二乗の場合だからか、二乗の場合の公式しか存在しませんけどね。
まあ、平方根使えばいいだけだと思いますけど。
公式は以下のようになっています。
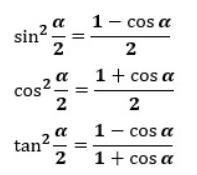
次項から公式の証明をしていきますが、二倍角の公式を使うだけで簡単に求めることができます。
2.sin2(α/2)の証明
まずはsin2(α/2)の証明から始めます。
二倍角の公式でcos2α=1-2sin2αとなることがわかっています。
この式を変形すると、sin2α=(1-cos2α)/2になります。
ここで、αをα/2に置き替えると公式の形になります。
これだけです。
3.cos2(α/2)の証明
次はcos2(α/2)の証明です。
sinの時とやることは変わりません。
二倍角の公式でcos2α=2cos2α-1となることがわかっています。
この式を変形すると、cos2α=(1+cos2α)/2になります。
ここで、αをα/2に置き替えると公式の形になります。
4.tan2(α/2)の証明
最後にtan2(α/2)の証明です。
tanα=sinα/cosαなので、tan2(α/2)=sin2(α/2)/cos2(α/2)になります。
先程の証明でsin2α=(1-cos2α)/2、cos2α=(1+cos2α)/2であることがわかっているので、これらを代入しただけです。
以上です。
求め方を知っていれば簡単に導き出せますが、単純に覚えろと言われると中々覚えにくい形の公式です。
二倍角の公式を覚えていれば導き出せるということだけでも覚えておけば問題ないと思いますよ?
以上、「半角の公式」についての説明でした。



