今回は、「“e”とは何なのか?」についての説明です。
1.初めに
数学の授業で習ったので何となく覚えている知識というものは結構あるかと思います。
昔習ったとしても仕事で使わなければ普通に忘れますからね。
今回は指数・対数の話になると出てくる“e”とは一体何だったかを整理していこうと思います。
2.“e”は複利計算の為に考え出された
“e”はネイピア数[Napier’s constant]と呼ばれています。
数値で表すと2.718282828459…と延々と続いていきます。
大体2.7くらいだと覚えておきましょう。
この数値は、以下の式から導き出されます。
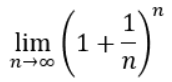
この式は何の式なのかと言うと、利子の複利計算をするためのモノです。
利子には利率と付与期間があります。
例えば、年利100%で付与期間が1年の銀行に1000円を預けた場合、1年後には2000円になります。
※ 非現実的な利率ですが、例なので気にしないでください。
では、年利100%で付与期間が半年になるとどうなるかと言うと、付与期間が2回に増える代わりに各利率が50%になります。
つまり、半年ごとに元金が1.5倍になります。
なので、半年で1000×1.5=1500円、その1500円を元金にしてもう半年後に1500×1.5=2250円になります。
付与期間が増えれば増えるほど得られる金額も増えていくんですね。
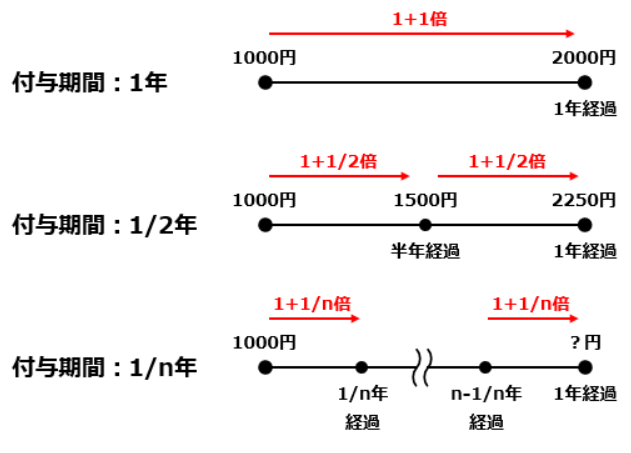
では、付与期間を限りなく短くしていくと最終的に得られる金額はどうなるのでしょうか?
そんな疑問の答えとなる関係式がこのlimの式になります。
試しに書いてみると本当にこの式通りになっているんです。
この式は元金を1、利率を1、付与期間を1/n(年)としています。
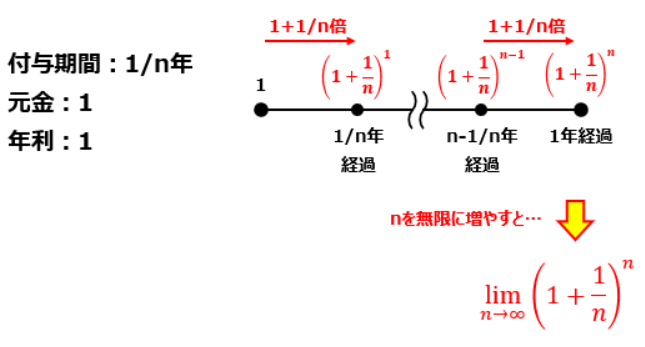
試しに代入してみると以下のようになります。
n=1(付与期間1年)の時、(1+1)1=2
n=12(付与期間1ヵ月)の時、(1+1/12)12=2.61303529
n=365(付与期間1日)の時、(1+1/365)365=2.714567482
n=1とn=12の結果を見比べると大きく変化していますが、n=12とn=365の結果を見比べると変化量が小さくなっていますね。
このように、付与期間を短くしていくと変化量が小さくなり、最終的にはある値に収束します。
この収束する値が“e”です。
要するに、利子を使って最大限に儲ける条件を考えた際の最終値がネイピア数になるのです。
ちなみに、年利が1ではなくxの場合はexに収束します。
特に覚える必要はないですが、ネイピア数はジョン・ネイピアが発表した資料に載っていたのが起源で、使い始めたのはレオンハルト・オイラーだと言われています。
また、利子の複利計算についてはヤコブ・ベルヌーイが行ったものです。
3.何故“e”なのか?
“e”の起源はふんわりと理解できたと思います。
では、一体どこから“e”が出てきたのでしょうか?
こういったケースの場合、大体英語表記した際の頭文字を取っていますが、ネイピア数を英語表記にしても“e”にはなりそうもないですよね?
諸説は多々ありますが、指数[exponential]の[e]だという説が有力なようです。
有力というだけで、確定ではないことには注意してくださいね。
4.“e”の性質
利子の複利計算から生まれた“e”ですが、数学の世界では自然対数の底に使用されていたり、指数関数で出てきたりします。
高校~大学の勉学では寧ろそちらの使われ方が一般的ですよね。
演算する上で便利な性質をいくつも持っているので、逆に“e”を使って物事を定義したりもするようです。
演算する上で“e”の持っている性質は以下の通りです。
- 指数関数exを微分すると元と同じexになる。
- 指数関数eの自然対数log(e)は1になる。
この辺りは指数と対数の説明時に深掘りしていくと思います。
ちょくちょく“e”の説明に「自然」というワードが出てくることが気になっている方もいるかもしれませんが、これには理由があります。
と言うのも、自然界では指数関数であるexの形を取って量が変化することが多いのです。
例えば、水の温度上昇と時間の関係なんかが該当します。
不思議なものですよね。
このように物理現象にはexが頻繁に関わってくるので、“e”に関する微分・積分・指数・対数の演算は結構重要になってきます。
以上、「“e”とは何なのか?」についての説明でした。




