今回は、「比例と反比例」についての説明です。
1.初めに
比例と反比例という概念は中学くらいで学ぶんでしたっけ?
いつ頃習ったのかは忘れましたが、本ブログでは初歩的な内容まで説明を網羅することを心掛けています。
なので、比例と反比例とはどんなものなのかを今回はまとめてみました。
2.比例とは?
比例[proportional]とは、2つの量の比が等しいことです。
例えば、1個10円の飴玉があったとします。
この飴玉を2個買うと20円、3個買うと30円になりますよね?
つまり、飴玉の個数が2倍になれば値段も2倍に、飴玉の個数が3倍になれば値段も3倍になるわけです。
この関係を比で表すと、飴玉1個:値段10円=飴玉2個:値段20円=飴玉3個:値段30円という具合に表せるので、何れも1:10の関係になっていることがわかります。
この関係のが「2つの量の比が等しい」状態になります。
なので、この関係を比例と呼びます。
では、飴玉をX個買うと何円になるかと言うと、10円がX個なので10X円になります。
ここで、飴玉をX個買った時の値段をY円と置くと、Y=10Xという関係になっていることがわかります。
2つの量を式で表した際に、Y=○Xという形で表現できると比例の関係になります。
この○に入る数値のことを比例定数と言います。
3.反比例とは?
反比例[inverse proportional]とは、2つの量があった時、片方の量の変化の倍率に対してもう一方の量の変化の倍率が逆数になることです。
言語化が異様に難しいので砕けた言い回しにすると、ある数を2倍にするともう片方の数は1/2倍に、ある数を3倍にするともう片方の数は1/3倍になるような関係のことを反比例と呼びます。
例えば、面積が16cm2の長方形があったとします。
この長方形の縦幅をXcm、横幅をYcmとした時、どんなパターンがあるでしょうか?
キリの良い数字では以下のようなパターンがあります。
(X,Y)=(1,16),(2,8),(4,4),(8,2),(16,1)
この組み合わせなら、どれも面積が16cm2になります。
この関係を横並びにしてみると、図1のような関係になっていることがわかります。
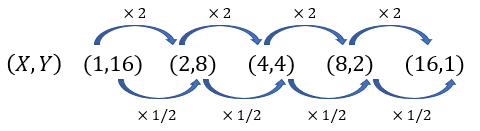
Xが2倍になればYが1/2倍、Xが4倍になればYが1/4倍というようになっているでしょう?
これが反比例です。
XとYの関係を式で表すと、以下のようになります。
X×Y=16
Y=16/X
2つの量を式で表した際に、Y=○/Xという形で表現できると反比例の関係になります。
以上、「比例と反比例」についての説明でした。



