【数学の雑学】 平方根とは？√の計算方法について解説！

今回は、「平方根」についての説明です。

１．平方根とは？二乗根とは？自乗根とは？

a、bという数字があったとして、a²=bを満たすaをbの平方根へいほうこんと呼びます。
二乗根にじょうこんや自乗根じじょうこんとも呼びます。

a²とはa×aのことで、「aの二乗」と呼びます。
言葉で表すとわかりづらいですよね。

２．例題

実際に数字を当てはめて考えてみましょう。

数字を当てはめると『あ、それだけ？』と感じるかもしれません。
それだけです。

『Aの平方根を求めよ』を『2乗してAになる数字を求めよ』に言い直せばすんなり理解できるのではないでしょうかね？

ちなみに、平方根には「正の平方根」と「負の平方根」があります。
正の平方根は符号がプラス、負の平方根は符号がマイナスです。
マイナスとマイナスをかけるとプラスになる関係から負の平方根も存在しています。

では、2の平方根は何でしょうか？
答えは、「±1.414…」と無限に続きます。
つまり、キリの良い数字になりません。
このようなキリの悪い数字を簡単に表す方法に「√ルート」というものがあります。

３．√について

「√」は根号こんごうとも呼ばれます。
平方根を表している記号のことです。

2の平方根の話の続きです。
2の平方根は「±1.414…」ですが、√を使用することで以下のように表せます。

「√2²」は、『√るーと2の2乗じょう』と読みます。

√は平方根を表している記号のことなので、2乗になる数字であれば√を取り外すことができます。
つまり、以下のような関係が成り立っています。

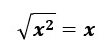
例として、16の平方根を求めてみましょう。

4の2乗が16ですので、√を取り払って平方根は±4だとわかりました。

次に、32の平方根を求めてみましょう。

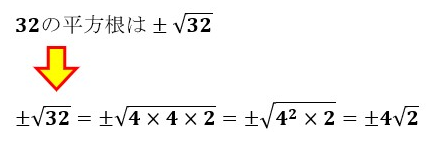
このように、2乗できる数字のみ√を取り外して表記します。

ここまで理解できれば平方根についての考え方は問題ないです。
中学生までは。

４．2乗してマイナスになる数

普通、2乗したら正の数になりますよね？

ですが、高校で習う数学から「2乗したら負の数になる本来存在しない数」である「虚数」というものが登場します。
虚数は数学の世界では「i」と書き、電気の世界では「j」と表します。

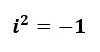
この考え方があると便利なことがあるので、深く考えずに『そういうものだ』と考えましょう。

以上、「平方根」についての説明でした。

---