今回は、「関数の割り算になっている場合の微分」についての説明です。
1.関数の割り算になっている場合の微分
前回は関数の掛け算に対する微分の説明をしたので、今回は割り算の説明をしていきます。
まずは結論から書いていきます。
f(x)とg(x)という関数があったとして、それらの商(※割り算のこと)を微分する場合は以下のような関係になります。
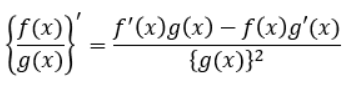
数学が嫌いな人は見るだけで頭が痛くなりそうな見た目をしてますね(笑)
では、以下のように書き換えてみたらどうでしょうか?
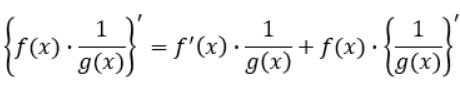
関数同士の割り算を掛け算の形で表したので、関数同士の掛け算の関係式に従って片方の関数を微分したものにもう片方の関数をそのまま掛けたもの同士を足し合わせました。
この式を整理していくと、最初の頭が痛くなりそうな関係式を導き出すことができます。
つまり、極論を言えば関数の割り算の関係式を覚えていなくても別に問題はありません。
掛け算の関係式さえ覚えておけば結果は導き出せますからね。
まあ、覚えておくと計算が速くなるというメリットはあるので、できるなら覚えておいた方が良いですけどね。
2.分数の微分
関数の掛け算の微分の関係式さえ知っていれば割り算もどうとでもなると述べましたが、{1/g(x)}’部分の計算方法がどうなるかわかるでしょうか?
おそらくよくわからないのではないかと思いますので、分数の微分について補足説明していきます。
と言ってもやることは単純で、先程同様に割り算を掛け算の形に変更して、関数の掛け算の微分を行うだけです。
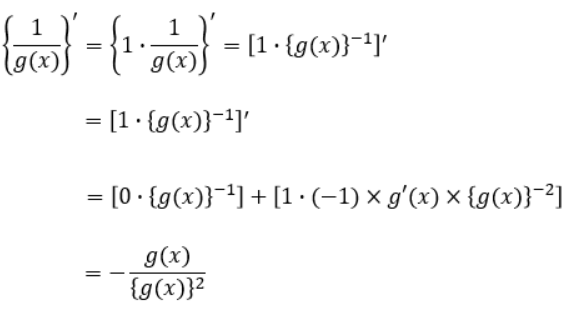
これで分数の微分がどうなるかはわかりましたね。
この関係を盛り込めば、公式が求められるわけです。
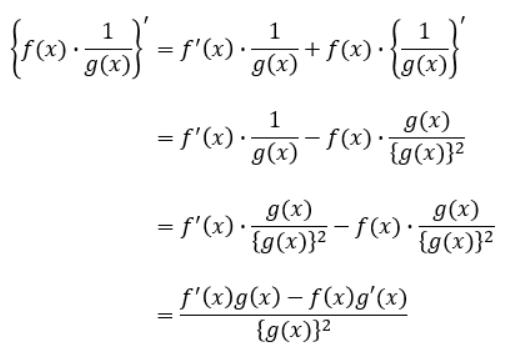
3.微分の定義に則った関係式の導き方
覚える必要があるかは微妙なところですが、どうやって割り算の微分の関係式である式1を導き出しているのかを記述していきます。
f(x)という関数を微分する場合の定義は以下のようになっていました。
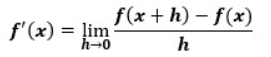
この定義に則ると、関数同士の割り算の場合は以下のようになります。
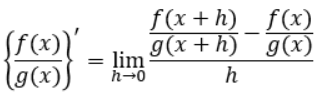
この式を変形していきます。
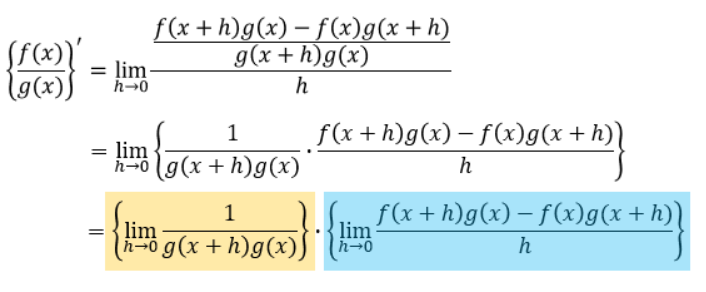
ここからは、橙塗り箇所と青塗り箇所に分けて考えていきます。
橙塗り箇所においてhを限りなく0に近づけていくと、分母がg(x)×g(x)になることがわかりますね?
なので、橙塗り部分は1/{g(x)}2になります。
青塗り箇所は、分子にf(x)g(x)-f(x)g(x)を加えてみます。
一見無駄なことのように感じるかもしれませんが、まあ見ていてください。
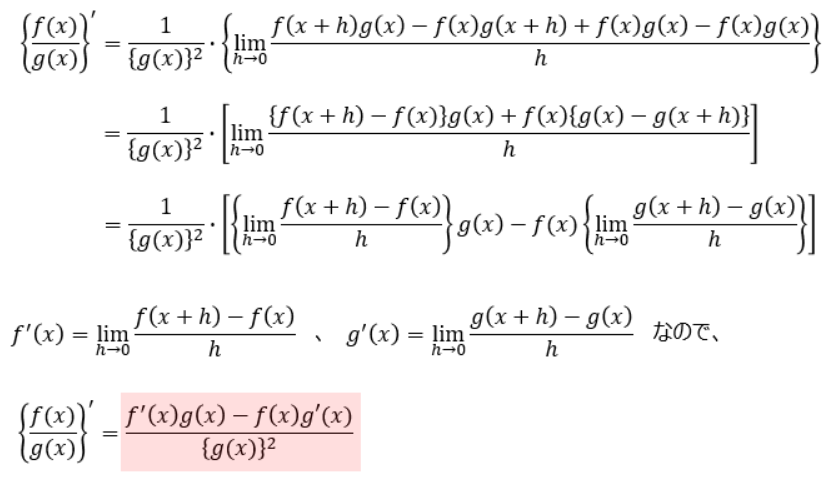
これで関係式を導くことができました。
以上、「関数の割り算になっている場合の微分」についての説明でした。




