今回は、「三角関数の微分」についての説明です。
1.三角関数の微分の関係式
ある点の傾きを求めることを微分と呼ぶわけですが、三角関数に対しても微分は可能です。
三角関数とは、いわゆるsin・cos・tanのことです。
三角関数についてよくわかっていない方・もう忘れたという方は、以下の記事から先に読んでみてください。
三角関数の微分の関係式は以下の通りです。
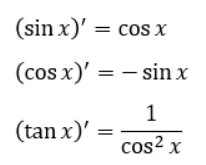
tanの微分結果の見た目に一瞬拒否反応が起きるかもしれませんが、理屈は単純なので安心してください。
どうしてこうなるかは次の項から証明していきますね。
2.sinの微分
まずはsinの微分の証明からです。
微分の定義は以下のようになっていましたよね?
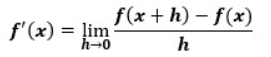
変数hを限りなく0に近づけた時の傾きが微分でした。
この定義を三角関数に当て嵌めて考えていきます。
f(x)=sinxという式を考えた場合、変化するのはxです。
つまり、三角関数の場合は角度が変化するわけです。
なので微分の式は以下のような形になります。
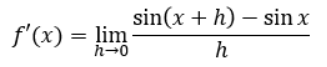
ここで、加法定理のsin(α+β)=sinαcosβ+cosαsinβの関係を適用します。
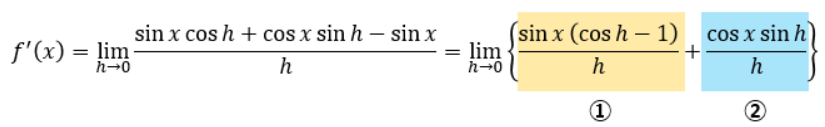
上記の①と②がそれぞれどうなるか計算していきます。
まずは①からです。
sinx以外の部分を変形していきます。
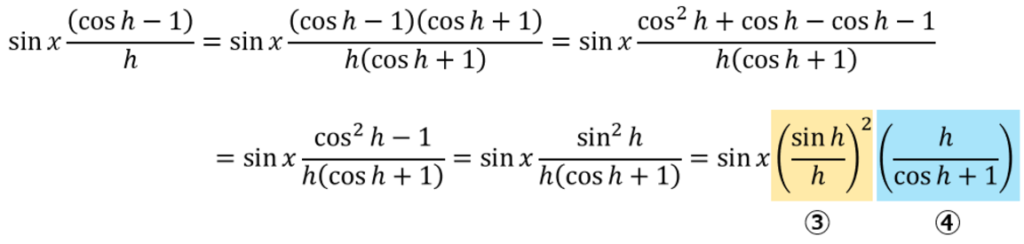
④を抜き出して考えると、h→0の時に分子は“0”に近づき、分母はcos0+1で“2”に近づくことがわかります。
つまり、④は“0”になります。
“0”に何をかけても“0”なので、結果として①は“0”になります。
次に②について考えていきます。図1のような図形があります。
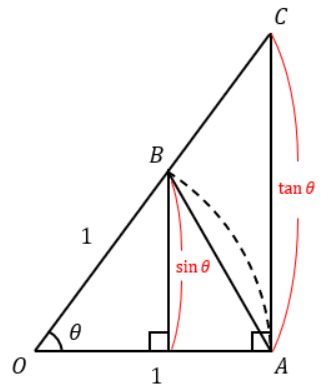
線分OA及び線分OBはどちらも長さが“1”で、扇形OABは単位円の一部を抜き出したような形状になっています。
この図において、面積は△OAB<扇形OAB<△OCAになっています。
それぞれの図形の面積は、以下のような関係になっています。
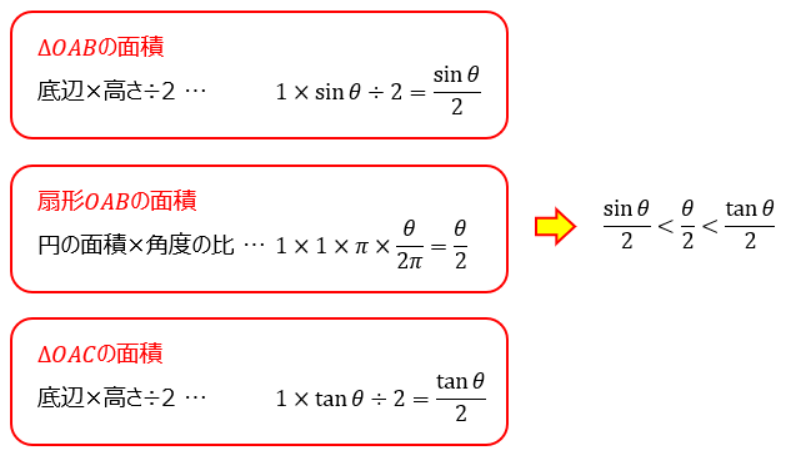
この関係式を変形していきます。

これでsinθ/θの極限θ→0が“1”になることがわかりました。
では、②を改めて見てみましょう。
今求めた関係のθがhに置き換わっただけの部分が存在しますよね?
なので、その部分は“1”になって②としてはcosxのみ残ります。
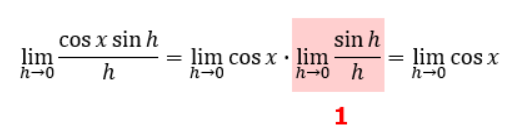
つまり、①+②はcosxしか残らないので、最終的にh→0という条件でcosxの極限を求めることになります。
ただ、cosxにhは関係しないので、hを0に近づけたところでcosxに変化はありません。
結果、f'(x)=cosxとなります。
これで、sinを微分するとcosになるという証明ができました。
ちなみに、sinθ/θの極限θ→0はθ→+0(プラス方向から“0”に近づける)でもθ→-0(マイナス方向から“0”に近づける)でも結果は変わりません。
関数によっては結果が異なることもありますが、この式の場合はθ→-0で考えてもsin(-θ)/(-θ)=(-sinθ)/(-θ)=sinθ/θと結局θ→+0の場合と同じ式になりますからね。
3.cosの微分
次はcosの微分です。
sin同様に微分の定義から計算することも可能ですが、sin(θ+90°)=cosθの関係を利用しても計算できますので、簡単な方で導いていきます。
この関係式について詳しく知りたい場合は以下の記事をご覧ください。
合成関数g(f(x))=sin(x+π/2)、f(x)=x+π/2、g(x)=sinxだと考えて微分していきます。
合成関数の微分はg'(f(x))f'(x)=cos(x+π/2)×1=cos(x+π/2)、cos(θ+90°)=-sinθなので、g'(f(x))f'(x)=-sinx。
これでcosの微分が-sinになることがわかりました。
4.tanの微分
最後にtanの微分です。
sinとcosの微分結果は既に証明済みなので、tanx=sinx/cosxの関係を利用して普通に微分していけばOKです。
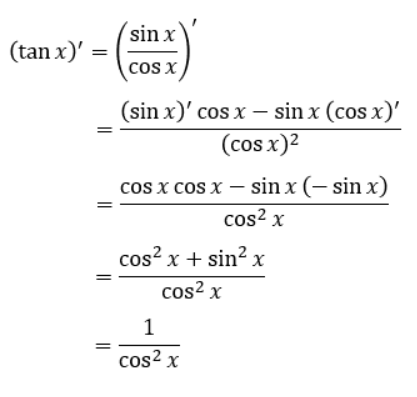
以上、「三角関数の微分」についての説明でした。





