今回は、「合成関数の微分」についての説明です。
1.合成関数とは?
f(x)=x+2、g(x)=x2という関数があったとします。
ここで、g(x)のxをf(x)に置き換えたとすると、g(f(x))={f(x)}2=(x+2)2という形になります。
このg(f(x))という考え方が合成関数です。
2つの関数を組み合わせ・合成しているから合成関数という単純な名称です。
合成関数は(g◦f)(x)という具合に小さな丸を使用して表されていることもあります。
この例の場合、g(x)の中にf(x)が入っているという表示となります。
f(x)=sinx、g(x)=3xならば(f◦g)(x)=sin3xという具合に、大体の関数は何かしらの合成関数となっています。
2.合成関数の微分
合成関数g(f(x))の微分は以下のようになります。
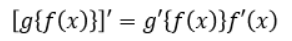
g'(x)のxをf(x)に置き換えたものとf'(x)を掛け合わせた値が合成関数の微分の結果になります。
この形からいきなり察しろと言われても意味不明だと思うので、実際に何パターンか微分の例を見てみましょう。

慣れてしまえばそんな複雑なものでもないですね。
3.関係式の導き方
覚える必要があるかは微妙なところですが、どうやってその関係式を導き出しているのかを記述していきます。
f(x)という関数を微分する場合の定義は以下のようになっていました。
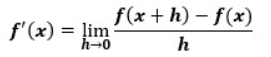
この定義に則ると、合成関数の場合は以下のようになります。
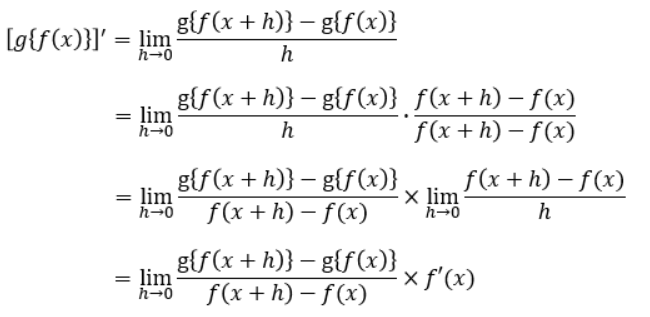
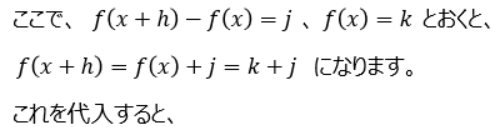

これで関係式を導き出すことができました。
以上、「合成関数の微分」についての説明でした。




