今回は、「C言語/データ型の種類と2進数のビット演算」についての説明です。
目次
1.初めに
前回、数学に関する関数について説明しましたので、同じ数学関連ということで2進数に関係した演算についても解説していこうと思います。
2進数について詳しくない方は、以下の記事を参考にしてみてください。
ちなみに、今回は数学に関連したライブラリである「math.h」は不要です。
2進数がどのように表現されて、どのような演算が存在するのか…という説明になります。
2.データ型の補足説明
まずは、2進数の表現方法について説明していきます。
2進数を表現するデータ型は?
これまでの記事で、データ型というものについて説明してきました。
intは整数の入れ物、doubleは実数の入れ物、charは文字の入れ物というヤツです。
2進数の場合、簡単なものについてはunsigned charを使用します。
unsignedの意味は一旦置いといて、『数字なのに何故char?』と疑問に思うのではないでしょうか?
ただ、よく考えてください。
アルファベットや数字も文字なんですよ。
なので、charで数字を表現することもできます。
charは、厳密には“1Byte(8bit)のメモリを使用することで文字を表現するデータ型”です。
1bitとか言われてもよくわからないという方は、ここでは0か1という数字1個を入れるための箱が1bitなのだと思ってください。
なので、“01”を表現したいなら2bit、“0011”を表現したいなら4bit、“00001111”を表現したいなら8bitのメモリが必要になるということになります。
なので、charなら8桁の2進数までなら表現できるというわけです。
signedとunsignedの違い
[unsign]とは[符号無し]という意味です。
なので、unsigned charは“符号無しで1Byte(8bit)のメモリを使用することで文字を表現するデータ型”ということになります。
逆に、signed charだと“符号あり”になります。
例えば、1Byte(8bit)の“11111111”という2進数が存在したとします。
この2進数をunsigned charで表現していた場合、そのまま“11111111”になります。
10進数でいう255です。
その為、unsigned charは0~255の範囲の値を表現できます。
それに対して、signed charで表現していた場合、考え方がガラッと変わります。
まず、最上位bit(一番左のbit)は符号を表現するために使用します。
最上位bitが0ならプラス、1ならマイナスとなります。
なので、数値と認識されるのは最上位bitを除いた7bitになる…とも言い切れません。
それは符号がプラスの場合だけで、マイナスの場合は全く異なります。
最上位bitが0で符号がプラスなら、そのまま7bitを読み取りましょう。
“01111111”なら10進数でいう+127になります。
この時点でunsigned charとは結果が全く違うんですよね。
最上位bitが1で符号がマイナスだった場合、その2進数は2の補数で表現されています。
2の補数の説明をするには先に1の補数について知っておく必要があります。
1の補数とは全bitを反転させたものを指しています。
例えば、“00000001”の1の補数は“11111110”になるわけです。
1の補数という名前の由来は、「足し合わせるとすべてが1になるように補う数だから」と言われています。
“00000001”に1の補数の“11111110”を足すと、“11111111”のように全部1になるでしょう?
2の補数は、この1の補数に1bit足したものとなります。
つまり、1の補数が“11111110”なら、2の補数は“11111111”になります。
従って、signed charにおける“11111111”は、符号がマイナスになった“00000001”ということになり、10進数では-1になります。
まとめると、最上位bitが1の時は符号がマイナスになり、数値としては1bit引いた後に1の補数を求めれば良いということになります。
この考え方に則ると、“10000000”が-128で最小値となります。
“10000000”(符号がマイナス) → “01111111”(-1bit) → “10000000”(1の補数) →-128
上記のようなルールになっているので、signed charの場合は-128~+127という何とも言えない範囲内で数値を表現できることがわかります。
なので、わかりやすいunsigned charがよく用いられているわけです。
ちなみに、charの場合はsignedとunsignedのどちらの扱いになるのかは未規定になっていて、コンパイラごとに定義されるようです。
その為、charだと0~256と-128~+127のどちらの範囲の数値を表現できるのかが曖昧になります。
charとsigned charとunsigned charに互換性は無いらしいので、char型はこの3種類が存在するのだと思っておきましょう。
主要なデータ型について
折角なので、他のデータ型の厳密な名称や表現範囲についてもまとめておきます。
| データ型種類 | 意味 | メモリ | 範囲 |
|---|---|---|---|
| unsigned char signed char | 符号無し文字型 符号付き文字型 | 1Byte | 0~255 -128~+127 |
| unsigned short int signed short int | 符号無し短整数型 符号付き短整数型 | 2Byte | 0~65535 -32768~+32767 |
| unsigned int signed int | 符号無し整数型 符号付き数型 | 4Byte | 0~4294967295 -2147483648~+2147483647 |
| unsigned long int signed long int | 符号無し長整数型 符号付き長整数型 | 4Byte | 0~4294967295 -2147483648~+2147483647 |
| unsigned long long int signed long long int | 符号無し長長整数型 符号付き長長整数型 | 8Byte | 0~18446744073709551615 -9223372036854775808~+9223372036854775807 |
| float | 単精度浮動小数点型 | 4Byte | |
| double | 倍精度浮動小数点型 | 8Byte |
実際はこんなルールになっているんです。
floatとdoubleは範囲を厳密に表そうとすると見た目がすごくなる上にそこまで重要ではないので、ブランク(空白)としています。
3.unsigned charを使用する
では、実際にunsigned charを使用してみます。
#include<stdio.h>
void main() {
unsigned char a = 0xf;
printf(“a=%x”, a);
}
unsigned charでaが0xfになるように指定しました。
0xfの“0x”の部分は、16進数を表します。
つまり、aは16進数で言うところのf(10進数の15,2進数の1111)を表していることになります。
この結果をprintfで表示する場合、変換指定子は以下のように対応しています。
16進数:%x
10進数:%d
8進数:%o
なので、【printf(“a=%x”, a);】の部分の変換指定子を%dに変更すれば、実行結果は「a=15」と表示されます。

『なんで2進数の変換指定子は載せてないの?』と思った方はいますでしょうか?
実は、2進数の変換指定子はありません。
なので、以降はビット演算をするものの、実際の数値としては16進数で表現されていくことに注意してください。
…なんで2進数に対応した変換指定子が無いんでしょうね?
4.2進数のビット演算
では、次は2進数のビット演算をしていきます。
ビット演算というとイメージがわかないかもしれませんが、ただ単に00001111という2進数のビットを00011110のようにズラしたりするだけです。
そんな調整がプログラミングで可能なのです。
そんなの用意するなら2進数に対応した変換指定子を用意して欲しい気もするけどね。
ビットをズラす
まずは例に出したビットをズラす方法です。
#include<stdio.h>
void main() {
unsigned char a = 0xf;
printf(“%xのビットを左に1つシフトさせると%xになる。\n”, a, a << 1);
printf(“%xのビットを右に1つシフトさせると%xになる。\n”, a, a >> 1);
}

6行目に【a << 1】、7行目に【a >> 1】と記載されていますよね?
これがビットをズラす指示です。
printfの文章からわかる通り、【a << 1】ならビットを左に1つシフトし、【a >> 1】ならビットを右に1つシフトします。
「<<」・「>>」の向きにビットがズレていくとイメージすれば良いです。
実際のプログラムの実行結果は以下の通りです。

まずは【a << 1】の効果の確認です。
元の数値は16進数で言うfなので、2進数では00001111を表しています。
ここからビットを左に1つシフトさせると00011110になります。
シフトした際に最小ビット(一番右の数字)は自動で0に切り替わります。
この2進数を16進数に直すと、「0001(1)」と「1110(e)」で1eになります。
同様に【a >> 1】の効果の確認です。
元の数値は2進数の00001111です。
ここからビットを右に1つシフトさせると00000111になります。
シフトした際に最大ビット(一番左の数字)は自動で0に切り替わります。
この2進数を16進数に直すと、「0000(0)」と「0111(7)」で07になります。
しっかりとビットがズレていることがわかりましたね。
ちなみに、【a << 2】なら「0011(3)」と「1100(c)」で3cになります。
数字の分だけビットがシフトする程度が変わるということです。
AND演算とOR演算
2進数のビットを用いたAND演算とOR演算も可能です。
『ANDとかORとか何?』と思った方は、以下の記事も参考にしてみると良いかもしれません。
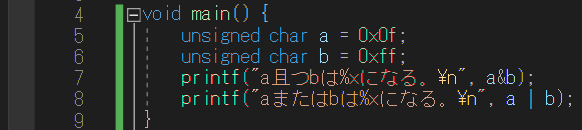
#include<stdio.h>
void main() {
unsigned char a = 0x0f;
unsigned char b = 0xff;
printf(“a且つbは%xになる。\n”, a&b);
printf(“aまたはbは%xになる。\n”, a | b);
}
過去の記事でif文とelse文の使い方について解説した際、【&&】が「且つ・論理積」、【||】が「または・論理和」を表すと説明しました。(以下の記事を参照)
これと同じで、7行目が「且つ・論理積」、8行目が「または・論理和」の関係になっています。
プログラムの実行結果は以下の通りです。
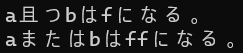
7行目を実行すると0f、8行目を実行するとffになるということになります。
今回はa(00001111)とb(11111111)の2数について比較を行っています。
7行目の論理積をすると、両方のビットが1なら1になります。
つまり、下位4ビットのみ1だと判断されるので、演算結果はf(00001111)になります。
8行目の論理和をすると、どちらか片方のビットが1なら1になります。
つまり、bが11111111になっているので、aが何であろうと演算結果はff(11111111)固定になります。
NOT演算
AND演算とOR演算の他にも、NOT演算も可能です。
NOT演算の場合、全ビットが反転します。
序盤に述べた1の補数を求めることができるわけです。
#include<stdio.h>
void main() {
unsigned char a = 0x0f;
printf(“aの全ビットを反転させると%xになる。\n”, (unsigned char)~a);
}

【~】という部分がNOT演算の記号です。
プログラムの実行結果は以下の通りです。

0f(00001111)のビットが反転したので、f0(11110000)になっていますね。
【~a】の前に【(unsigned char)】とくっついているのは、数値の桁が変わると結果が変わってしまうからです。
例えば、aは00001111と指定していますが、000000001111でも表現されている数値は同じになるでしょう?
ですが、後者の全ビットを反転させてしまうと111111110000(ff0)になってしまうので、演算結果が変わってしまいます。
だから、『ここで取り扱う値はunsigned char(8bit)ですよ!』と宣言しているわけです。
実際、【(unsigned char)】を取っ払ってプログラムを実行すると桁数がおかしくなります。
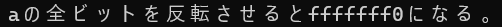
以上、「C言語/データ型の種類と2進数のビット演算」についての説明でした。






