今回は、「平行板コンデンサを並列接続する前後の静電エネルギーの総和の変化」についての説明です。
1.本記事で出てくる公式のまとめページリンク
W=CV2/2=QV/2=Q2/2C
Q=CV , C=εS/d
E=V/d
2.前置き
極板間距離がd[m]、極板面積がS[m2]のコンデンサAと、極板間距離がd[m]、極板面積が2S[m2]のコンデンサBがあったとします。
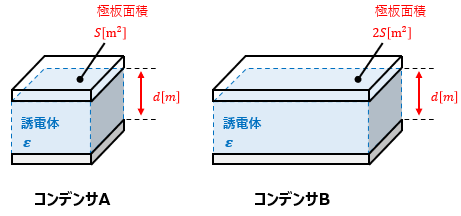
今、これらのコンデンサは極板間の誘電率が同じで、電界も同等になるように直流電源で充電されていたとします。
充電完了したコンデンサA及びBを並列接続して充分に時間が経過した時、各コンデンサに蓄えられている静電エネルギーの総和は並列接続前後で変化すると思いますか?
答えは、変化することがあります。
エネルギーが損失していないから静電エネルギーはなんとなく保存されるような気がするかもしれませんが、変化することがあるのです。
このような問題は電検三種の過去問にも登場していたりします。
今回は、静電エネルギーが実際にどう変化するのかを計算しつつ説明していこうと思います。
電荷と静電容量の関係式やコンデンサの静電エネルギーの公式などの前提知識は本ブログにまとめてあるので、見覚えの無い公式が出てきた場合は記事を遡って確認してみてください。
本記事の上の方に公式とリンクはまとめて記載しておきます。
3.コンデンサを並列接続する前後の静電エネルギーの総和の変化
まず、コンデンサA及びBが単独で存在する際の静電エネルギーを求めてみましょう。
コンデンサの静電エネルギーはCV2/2で表されます。
ですが、現状コンデンサA及びBの静電容量(C)と繋がっている電源(V)は不明なので、そこから考えていきます。
コンデンサAの静電容量をCとした場合、公式に当て嵌めることでC=εS/dと表すことができます。
同様に、コンデンサBの静電容量は、CB=2εS/d=2Cと表せます。
電界Eは同等なので、コンデンサAにかかる電圧をVとした場合、公式に当て嵌めることでV=Edと表すことができます。
同様に、コンデンサBにかかる電圧は、VB=Ed=Vと表せます。
以上より、コンデンサAの静電エネルギーはCV2/2、コンデンサBの静電エネルギーはCV2と表すことができます。
つまり、並列接続していない時のコンデンサA及びBの静電エネルギーの総和は、CV2/2+CV2=3CV2/2になります。
次は、並列接続した場合について考えていきます。
静電エネルギーは電荷Q’と静電容量C’のコンデンサの場合はQ’2/2C’と表すことが可能なので、ここに総電荷と合成容量を代入しようと思います。
Q=CVの関係より、コンデンサAが蓄えている電荷はCV、コンデンサBが蓄えている電荷は2CVです。
なので、並列接続した際の電荷の総量Q’はCV+2CV=3CVです。
コンデンサを並列接続した際の静電容量は純粋な足し算になります。
その為、並列接続した際の合成静電容量C’は3Cです。
これを最初の式に代入すると、Q’2/2C’=9C2V2/6C=3CV2/2となります。
よって、この例の場合は並列接続前後で静電エネルギーの総和に変化はないようです。
では、今度はコンデンサAと極板間距離が2d[m]、極板面積がS[m2]のコンデンサCの2つで同様の計算を行ってみたらどうなるか考えてみます。
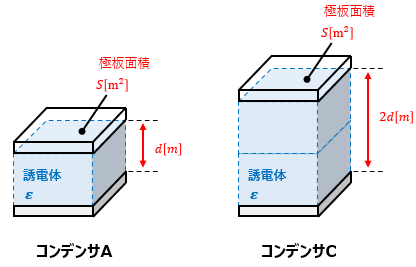
考え方は同じなので計算は大雑把にして省きますが、コンデンサCの静電容量はC/2、コンデンサCにかかる電圧は2Vになります。
よって、並列接続していない時のコンデンサA及びCの静電エネルギーの総和は3CV2/2に変化します。
同様に、並列接続した場合について考えると、総電荷が2CV、合成静電容量が3C/2、静電エネルギーの総和は4CV2/3になります。
この例の場合、並列接続前後で静電エネルギーの総和が変わっていますよね?
このように条件によっては変わったり変わらなかったりするので注意しましょう。
以上、「平行板コンデンサを並列接続する前後の静電エネルギーの総和の変化」についての説明でした。




