【基礎から学ぶトランジスタ】 ベース接地回路の入力信号波形に対する出力信号波形の求め方

今回は、「ベース接地回路の入力信号波形に対する出力信号波形の求め方」についての説明です。

１．ベース接地の特徴

ベース接地回路は、ベースを基準電圧としてエミッタに入力信号を入れ、コレクタから出力信号を取り出す回路です。

基本的な特徴は以下の通りです。

入力インピーダンス	：低い
出力インピーダンス	：高い
電圧増幅率	：高い
電流増幅率	：1倍
高周波特性	：良い
出力の位相	：非反転(同相)

２．ベース接地回路の入力信号波形に対する出力信号波形の求め方

ベース接地回路の入力信号に対する出力信号波形が、実際にどうなるのかを例題を用いて説明していきます。

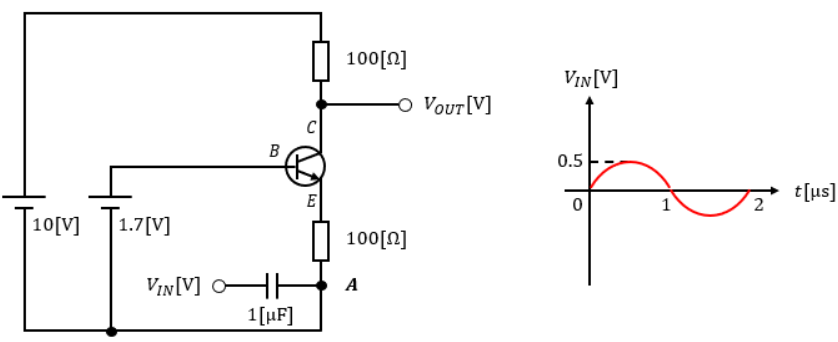
図1のような回路図及び入力信号V_INがあった場合の出力信号V_OUTを求めてみます。
前提条件として、トランジスタのベース－エミッタ間電圧V_BEは0.7[V]、電流増幅率h_FEは∞とします。
※入力信号の近くにある1[μF]のコンデンサは直流を通さないために置かれているだけで、回路動作に影響はありません。

入力信号V_INが0[V]の場合

まずは、入力信号V_INが0[V]の場合について考えます。
t=0,1,2[μs]の時ですね。

トランジスタのベース端子にかかる電圧V_Bは1.7[V]で固定されています。
エミッタ端子電圧V_E=ベース端子電圧V_B－ベース－エミッタ間電圧V_BEなので、V_E=1.7－0.7=1.0[V]になります。
なので、エミッタ端子の直流成分の電圧は1.0[V]だとわかります。

これに対して、点Aには交流である入力信号V_INが印加されます。
今回はV_IN=0[V]なので、点Aの電圧は0[V]となります。
つまり、エミッタ端子側の100Ω抵抗には1.0[V]の電圧がかかるので、オームの法則よりエミッタ電流I_Eは10[mA]になることがわかります。

電流増幅率h_FEが∞という条件より、エミッタ電流I_Eとコレクタ電流I_Cは等しいので、回路全体に10[mA]の電流が流れることがわかります。

回路に流れる電流が10[mA]だと判明したため、コレクタ端子側の100Ω抵抗にかかる電圧もオームの法則より、100[Ω]×10[mA]=1.0[V]と求めることができます。

コレクタ端子電圧V_Cはコレクタ端子に繋がっている電源電圧から100Ω抵抗の電圧降下を差し引いた値になるので、V_C=10-1=9[V]になります。

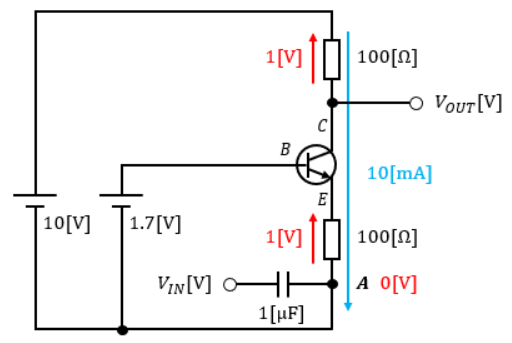
出力信号V_OUTはコレクタ端子電圧V_Cに等しいので、V_OUTは9[V]になるとわかります。
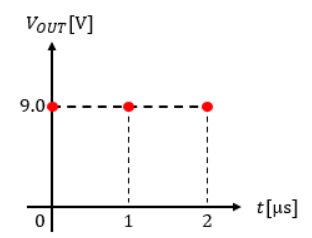
よって、出力信号をプロットすると以下のようになります。

入力信号V_INが0.5[V]の場合

次は、入力信号V_INが0.5[V]、t=0.5[μs]の時について考えます。

考え方は先程と全く同じです。
V_INが変化しているので、同じように当て嵌めていってみましょう。

エミッタ端子電圧V_Eは変化しないので、V_E=1.0[V]は共通です。
ただ、交流成分が変化しているので、点Aの電圧が0.5[V]に変化します。
つまり、エミッタ端子側の100Ω抵抗にかかる電圧は、エミッタ電圧V_Eと点Aの電圧の差分となります。
よって、1.0－0.5=0.5[V]となります。

この0.5[V]の電圧がエミッタ側の100Ω抵抗にかかるので、オームの法則よりエミッタ電流I_Eは5[mA]になることがわかります。

そして、エミッタ電流I_Eとコレクタ電流I_Cは等しいので、回路全体に5[mA]の電流が流れることがわかります。

回路に流れる電流が5[mA]だと判明したため、コレクタ端子側の100Ω抵抗にかかる電圧もオームの法則より、100[Ω]×5[mA]=0.5[V]と求めることができます。

コレクタ端子電圧V_Cはコレクタ端子に繋がっている電源電圧から100Ω抵抗の電圧降下を差し引いた値になるので、V_C=10-0.5=9.5[V]になります。

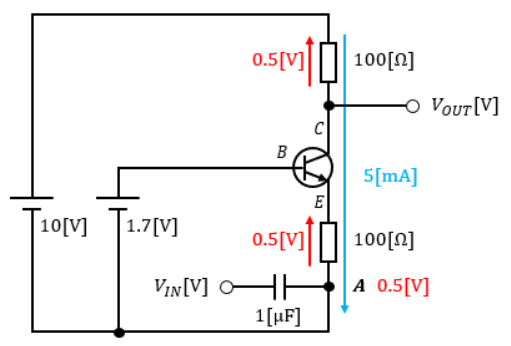
出力信号V_OUTはコレクタ端子電圧V_Cに等しいので、V_OUTは9.5[V]になるとわかります。
よって、出力信号をプロットすると以下のようになります。

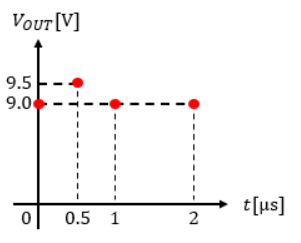
入力信号V_INが－0.5[V]の場合

最後に、入力信号V_INが－0.5[V]、t=1.5[μs]の時も同様に考えます。

エミッタ端子電圧VEは変化しないので、VE=1.0[V]は共通です。
ただ、交流成分が変化しているので、点Aの電圧が－0.5[V]に変化します。
つまり、エミッタ端子側の100Ω抵抗にかかる電圧は、エミッタ電圧V_Eと点Aの電圧の差分となります。
よって、1.0－(－0.5)=1.5[V]となります。

この1.5[V]の電圧がエミッタ側の100Ω抵抗にかかるので、オームの法則よりエミッタ電流I_Eは15[mA]になることがわかります。

そして、エミッタ電流I_Eとコレクタ電流I_Cは等しいので、回路全体に15[mA]の電流が流れることがわかります。

回路に流れる電流が15[mA]だと判明したため、コレクタ端子側の100Ω抵抗にかかる電圧もオームの法則より、100[Ω]×15[mA]=1.5[V]と求めることができます。

コレクタ端子電圧V_Cはコレクタ端子に繋がっている電源電圧から100Ω抵抗の電圧降下を差し引いた値になるので、V_C=10-1.5=8.5[V]になります。

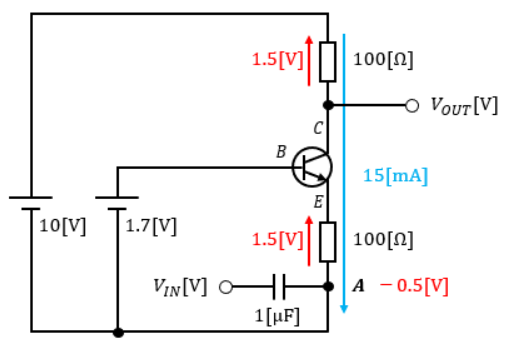
出力信号V_OUTはコレクタ端子電圧V_Cに等しいので、V_OUTは8.5[V]になるとわかります。
よって、出力信号をプロットすると以下のようになります。

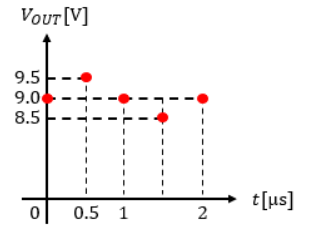
こうしてプロット箇所を増やしてプロット同士を結ぶと、出力信号波形が浮かび上がってきます。
結果、出力信号波形は以下のような形状になります。

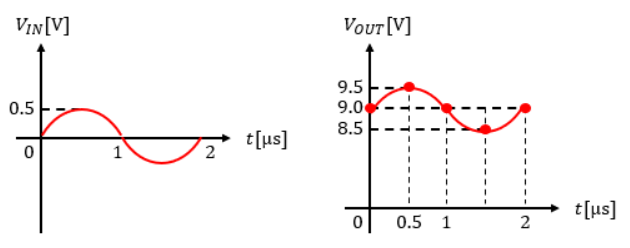
入力信号が増幅されて、出力の位相がそのままになっていることがわかりますね。

ちなみに、入力信号の印加箇所である点Aをエミッタ側の100Ω抵抗の上に移動するだけで得られる出力波形は全くの別物になるので注意が必要です。

以上、「ベース接地回路の入力信号波形に対する出力信号波形の求め方」についての説明でした。

---