今回は、「静電気に関するクーロンの法則」についての説明です。
1.静電気に関するクーロンの法則
「磁気に関するクーロンの法則」と併せて考えると覚えやすいです。
点とみなせるほど小さな電荷のことを点電荷と呼びます。
電荷を持った粒子が一点に集まっているとみなしたものとも言えます。
2つの点電荷に働く静電力(反発力・吸引力)の大きさF[N]は、2つの電荷q1とq2の積に比例し、距離の2乗に反比例します。
この関係を、静電気に関するクーロンの法則と呼び、静電力のことをクーロン力とも呼びます。
電荷の量記号はQもしくはq、単位は[C]です。
仮に真空中にq1=+q[C]とq2=-q[C]の点電荷が存在していた場合、図1のように静電力(ここでは正と負の異種電荷が存在している為、吸引力が発生)が働きます。
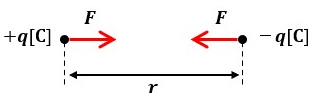
この時の静電力を式で表すと以下のようになります。
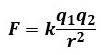
rは距離で、単位は[m]です。
電荷が真空中に存在している場合、kの値は以下のようになります。
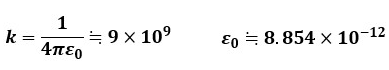
ε0は真空中の誘電率で、単位は[F/m]です。
εは「イプシロン」と読みます。
誘電率とは、媒質(空気などの物質が存在できる場所)の性質を表す定数です。
その媒質中ならどの程度静電力が発生しやすいかを表す定数と思っていただければ良いかと。
真空以外の媒質では誘電率εを用い、誘電率εが真空中の誘電率ε0の何倍かを表した比のことを比誘電率εsと呼びます。
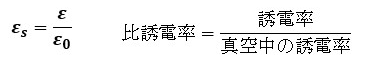
以上の点を踏まえて静電力の式を整理すると、次のように表すこともできます。
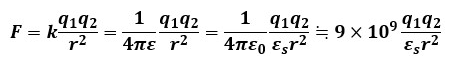
真空中の比誘電率εsは、ε=ε0となる関係からεs=1として計算することになります。
以上、「静電気に関するクーロンの法則」についての説明でした。



