【基礎から学ぶ電気回路】対称三相電圧と平衡負荷の間に負荷がある場合の考え方

交流には単相交流と三相交流が存在します。
この内、単相交流は一般家庭のコンセントに供給されていますが、三相交流は一般家庭で見かけることはありません。
三相交流は電気系の専門性が高くなるのです。
本記事では、そんな三相交流を理解できるようになることを目的としています。

今回は、「対称三相電圧と平衡負荷の間に負荷がある場合の考え方」についての説明です。

電源側が対称三相交流且つ負荷側が平衡負荷である回路のことを平衡三相交流回路と呼びます。
回路を構成する要素が対称三相交流と平衡負荷だけならわかりやすいのですが、電検3種などの問題では対称三相電圧と平衡負荷の間に負荷が配置されていることがあります。

問題を解きなれていれば何も迷うことはないのですが、初見だと相電圧・線間電圧・相電流・線電流の関係がごちゃごちゃしてよくわからなくなる可能性が高いです。

今回は、そんな場合の考え方を例題を解きながら解説していきます。

早速ですが、例題を解いていきましょう。

対称三相電圧と平衡負荷の間に負荷が配置されているというのは、図1のような状況を指しています。
なんか微妙な位置に負荷が配置されているでしょう？

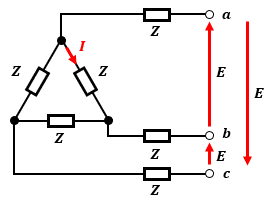
ここで、E=200[V]、Z・=12+j9[Ω]の時の相電流[A]の大きさを求めましょう。

まず、このままの形ではΔ結線回路の相電流Iを求められないので、Δ－Y変換をします。
平衡負荷(※ 同じインピーダンス)のΔ結線回路の場合、Δ結線回路を構成するインピーダンスの1つを3で割った値がY結線回路を構成するインピーダンスの1つになりますので、図2のようになります。

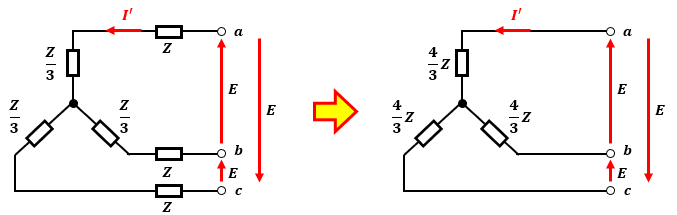
こうしてY結線回路にすることで、負荷をまとめて考えることができるようになります。
対称三相電圧と平衡負荷の間に負荷がある場合は大概Δ結線回路にされているので、まずはΔ－Ｙ変換して整理すると覚えておきましょう。

Z・=12+j9[Ω]なので、4Z/3=16+j12[Ω]の平衡負荷になっているわけです。
なので、合成インピーダンスの大きさは、√(16²+12²)=20[Ω]になります。

Eは線間電圧なので、相電圧は線間電圧の1/√3になるという関係から、200/√3[V]になります。

以上の関係から単相を取り出して考えてみると、相電流I’=相電圧÷インピーダンスの大きさ=(200/√3)÷20=10/√3[A]になります。

ここで求めた相電流I’は、Y結線回路の相電流であり、Y結線回路の線電流です。
Y結線回路の線電流は、そもそもの図1の回路の線電流と等しいです。
つまり、図1でいうところのΔ結線の線電流でもあります。

なので、Δ結線の相電流は線電流の1/√3になるという関係から、I=(10/√3)÷√3≒3.3[A]となります。

ただ読んでいるだけでは中々理解に苦しむかもしれませんので、自分で実際に解いてみることを推奨します。
問題で明らかにされているのが、相電圧・線間電圧・相電流・線電流のどれなのかをしっかりと整理することが大事です。

ちなみに、ここから更に平衡三相負荷の消費電力も求めようとすると、今度は力率が関係してきます。
交流回路はこの辺りが本当にややこしいので、少しでも疑問を感じたら振り返ることが大事です。

以上、「対称三相電圧と平衡負荷の間に負荷がある場合の考え方」についての説明でした。