今回は、「磁界中を三角形の導体に横切らせた時の誘導起電力の時間的変化」についての説明です。
1.誘導起電力の時間的変化を図示する練習問題
「フレミング右手の法則」の説明で、誘導起電力の向きや大きさについて簡単に触れました。
今回は、実際にどんな誘導起電力が発生するのかを例題を解きながら考えていきます。
※電験三種の過去問を参考にしています。
図1のように奥から手前方向に磁束密度B[T]の一様な磁界が存在して、磁界を横切らない位置(磁界が0)に正三角形の回路ループが存在していたとします。
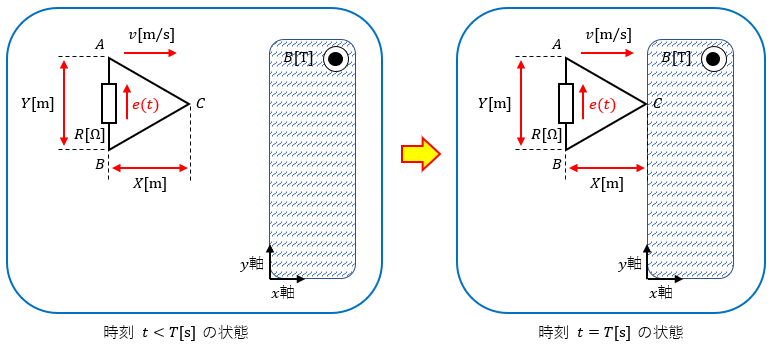
回路ループの辺ABはy軸と平行を保っているとします。
この状態で回路ループがx軸方向に速度v[m/s]で接近しているとします。
回路ループの点Cが磁界に侵入する瞬間の時間をT[s]とした時、抵抗Rに加わる誘導起電力e(t)の時間的変化を図示してみましょう。
t<Tの状態
まず、t<Tの時について考えます。
この状態では回路ループと鎖交する磁束は存在しませんので、誘導起電力は0[V]です。
まあ、当たり前ですよね。
回路ループと鎖交する磁束が存在する区間
次は、回路ループと鎖交する磁束が存在する区間について考えていきます。
回路ループは、t=T[s]から磁界に侵入します。
回路ループがx軸方向へ進むスピードはv[m/s]なので、回路ループが磁界に完全に侵入するまでにかかる時間はX/v[s]です。
なので、回路ループが磁界中に完全に入り込むまでの時間t[s]はT<t<T+X/vの間となります。
まずは、この区間の誘導起電力について考えます。
誘導起電力は導体と鎖交する磁束が変化する際に発生するものでした。
辺AC及び辺BCは速度v[m/s]で移動するので、鎖交する磁束は時間経過とともに直線的に増加していきます。
その為、辺AC及び辺BCが磁界に完全に侵入した時の誘導起電力を計算すれば、誘導起電力の時間的変化を図示可能です。
誘導起電力の発生する方向は、フレミング右手の法則から、辺ACはAからCの方向、辺BCはCからBの方向だとわかります。
なので、辺ACと辺BCに現れる誘導起電力の向きは同じです。
磁束密度B[T]の磁界中を導体が移動するので、磁束の変化量ΔΦはB×(導体が磁界中を横切った面積分)となります。
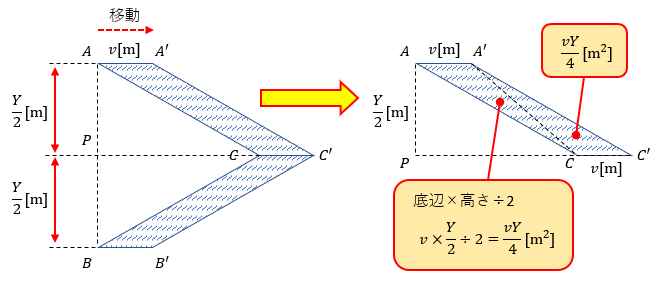
辺AC及び辺BCが1秒経過するとv[m]移動しますので、図2のように辺ACBが辺A’C’B’の位置まで移動します。
この時の平行四辺形AA’C’C及び平行四辺形BB’C’Cの面積は、底辺×高さ÷2×2でv×(Y/2)÷2×2=vY/2[m2]です。
なので、導体ACBが1[s]間に磁界中を横切る面積は、vY/2+vY/2=vY[m2]となります。
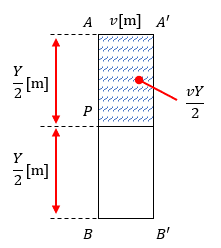
ちなみに、平行四辺形AA’C’C及び平行四辺形BB’C’Cの面積は、y軸方向の辺AP及び辺BPが磁界中を横切った場合の面積に等しいです。
x軸方向に平行な辺CPは磁界中を横切っても面が発生しないので当前のことなんですけどね。
以上より、1[s]間の磁束の変化量ΔΦはBvY[Wb]となります。
電磁誘導に関するファラデーの法則より、電磁誘導により発生する起電力の大きさe[V]は、コイルと鎖交する磁束の変化量に比例するとわかっています。
よって、t=T+X/vの時の誘導起電力の大きさはBvY[V]だと言えます。
この誘導起電力が抵抗Rの両端にかかります。
ただし、図1に示したe(t)の向きと誘導起電力による抵抗Rでの電圧降下の方向が逆になっているので、e(T+X/v)=-BvY[V]となります。
T+X/v<tの回路ループが完全に磁界中に入った状態
最後に、T+X/v<tの回路ループが完全に磁界中に入った状態について考えます。
辺AC及び辺BCの誘導起電力の大きさと向きはわかっているので、辺ABの誘導起電力を求めます。
とは言っても、辺ABは辺AP+辺BPなので、誘導起電力の大きさは先程の結果から計算するまでもなくBvY[V]だとわかります。
問題は向きです。
フレミング右手の法則で誘導起電力の向きを確かめてみると、AからBの方向だとわかります。
これって、辺AC及び辺BCに発生する誘導起電力と向きが逆になっていますよね?
つまり、辺ABに発生する誘導起電力と辺AC及び辺BCに発生する誘導起電力は互いに打ち消し合います。
すると、誘導起電力はちょうど0[V]になります。
ここまでの関係を図示すると、誘導起電力は図4のように変化することがわかります。
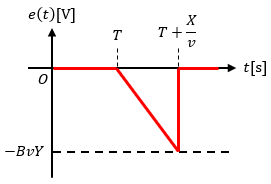
導体が横切った際に面ができる方向と誘導起電力の発生する向きには注意しましょうね。
以上、「磁界中を三角形の導体に横切らせた時の誘導起電力の時間的変化」についての説明でした。




