今回は、「最大電力の求め方」についての説明です。
1.ポイント
起電力E、内部抵抗rで構成される電源に抵抗Rを繋いだ時に抵抗Rに発生する電力が最大になる条件は内部抵抗r=抵抗R。
その時の最大電力Pm[W]はE2/4rとなる。
2.最大電力
起電力E、内部抵抗rで構成される電源に抵抗Rを繋いだ時、抵抗Rに発生する電力が最大になる条件は内部抵抗r=抵抗Rです。
では、何故内部抵抗r=抵抗Rの時に電力が最大になるかを考えてみましょう。
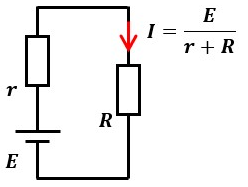
図1は、起電力E、内部抵抗rで構成される電源に抵抗Rを繋いだ回路です。
抵抗Rでの消費電力Pは以下のように表せます。
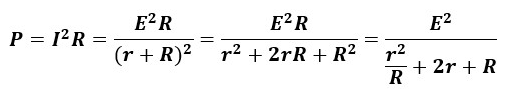
この式から、分母が小さければ小さい程電力が大きくなることがわかります。
つまり、分母が最小になる時に電力が最大になるということです。
分母を構成している中で変数はRのみなので、Rの値がいくつの時に分母が最小になるかを考えます。
分母の第2項の2rは定数ですので、変数であるRを含む分母の第1項r2/Rと第3項Rの和が最小の時に電力が最大になります。
突然ですが、最小定理をご存じでしょうか?
「2つの正の数(以降は2数と呼びます)があり、2数の積が一定である場合、2数が等しい時に2数の和が最小になる」という定理です。
以下に例を示します。

最小定理のイメージはできたかと思います。
何故唐突に最小定理の説明を始めたかというと、r2/RとRの2数にも最小定理が適用できるからです。
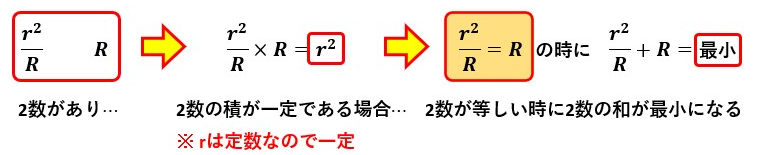
つまり、r2/R=Rの時に分母が最小になり、電力が最大になります。
この式を整理するとr=Rとなるので、抵抗Rに発生する電力が最大になる条件は内部抵抗rが抵抗Rと等しくなることだと言えます。
以上が、内部抵抗r=抵抗Rの時に電力が最大になる理由です。
ちなみに、最大電力Pmはr=Rの関係から以下のように表せます。
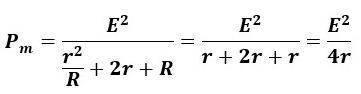
以上、「最大電力の求め方」についての説明でした。




