今回は、「差動増幅回路」についての説明です。
1.差動増幅回路とは?
トランジスタを使用した特殊な回路の中に、差動増幅回路というものがあります。
この回路は、2つの入力信号の差分を増幅して出力する回路です。
差動増幅器と呼ばれていることもあります。
何れも名称そのままですね。
差動増幅回路自体はオペアンプでも組むことができるのですが、オペアンプを使用している場合は減算回路とも呼ばれます。
トランジスタを用いた差動増幅回路は、npn型トランジスタを使用したものとpnp型トランジスタを使用したものの2種類があります。
npn型トランジスタを使用した場合とpnp型トランジスタを使用した場合では、以下のように接続が変化します。
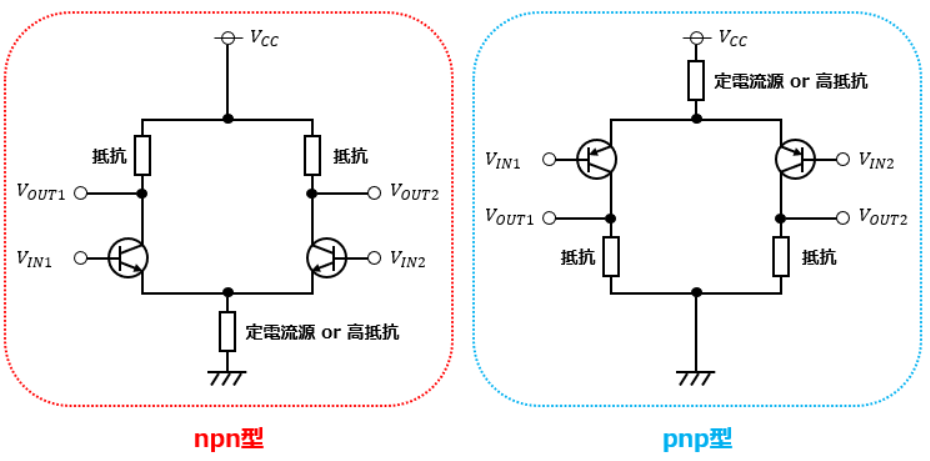
npn型もpnp型も、全く同じ特性のトランジスタを使用して、エミッタ端子同士を繋いだ先に定電流源または高抵抗を配置します。
このような回路構成にして、2つのトランジスタに流れる電流(コレクタ電流)の総和を一定に保つのが鍵です。
今回は、例としてnpn型トランジスタを利用した差動増幅回路の動作原理を簡単に解説していこうと思います。
2.差動増幅回路の考え方
npnトランジスタを使用した差動増幅回路の電流・電圧を以下のように置きます。
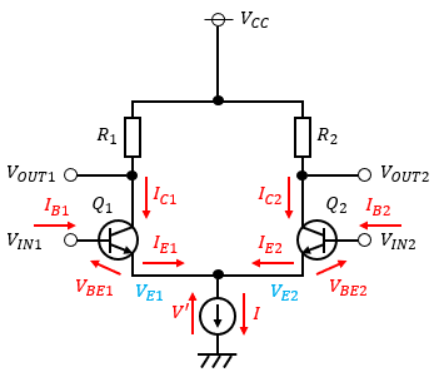
ICはコレクタ電流、IEはエミッタ電流、VBEはベース-エミッタ間電圧です。
トランジスタは2つ存在するので、向かって左を“1”、右を“2”にナンバリングしました。
前述の通り、トランジスタQ1とQ2の特性は全く一緒です。
結論から述べると、入力信号VIN1とVIN2の電位差によって、出力電流(ここで言うコレクタ電流IC)は以下のように変化します。
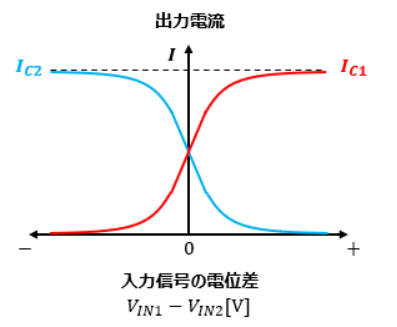
入力信号VIN2に対してVIN1が大きくなるほど出力電流IC1が大きくなり、入力信号VIN1に対してVIN2が大きくなるほど出力電流IC2が大きくなっていますね。
入力信号の電位差に応じて増幅される出力信号は変化するわけです。
出力電流の最大値は定電流Iとなります。
では、何故このような動作をするのか見ていきましょう。
各トランジスタの電流増幅率hFEは∞とします。
差動増幅回路の見た目はごちゃごちゃしているように見えますが、動作自体は結構単純なのであまり身構えないでくださいね?
まず、定電流I=エミッタ電流IE1+エミッタ電流IE2になっているのは見てわかりますよね?
キルヒホッフの第一法則です。
では、エミッタ電流IE1≒コレクタ電流IC1、エミッタ電流IE2≒コレクタ電流IC2になっていることはわかるでしょうか?
電流増幅率hFEは、コレクタ電流ICをベース電流IBで割った値に等しいです。
その電流増幅率hFEが∞ということは、ベース電流IBに対してコレクタ電流ICは非常に大きいということになります。
エミッタ電流はコレクタ電流+ベース電流なので、IE1=IC1+IB1≒IC1となるわけです。
つまり、定電流I=コレクタ電流IC1+コレクタ電流IC2という関係が成り立っています。
だから出力電流(コレクタ電流IC1及びIC2)の最大値は定電流Iとなりますし、片側の出力電流が上がるともう片側の出力電流が下がるのです。
上記の関係を加味して出力信号VOUT1及びVOUT2を式で表すと、以下のようになります。
VOUT1=VCC-R1IC1
VOUT2=VCC-R2IC2
先程、片側の出力電流(コレクタ電流)が上がるともう片側の出力電流が下がると言いましたよね?
ということは、以下のような関係が成り立っていると言えます。
IC1上昇⇒IC2減少⇒VOUT1減少、VOUT2上昇
IC1減少⇒IC2上昇⇒VOUT1上昇、VOUT2減少
差動増幅回路の原理はこれだけです。
トランジスタの基本的な考え方しか使っていないでしょう?
3.練習問題
文字ばかりだと理解しづらいかもしれないので、実際に練習問題を解いてみましょう。
図2と同じ回路に以下のような数値を対応させました。
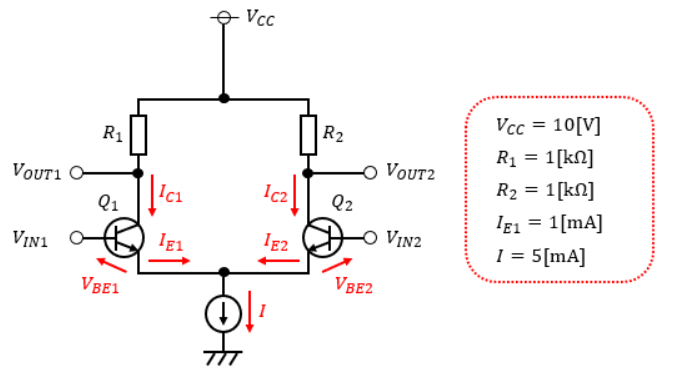
トランジスタQ1とQ2の特性は同じで電流増幅率hFEは∞、VIN1-VIN2=-0.05[V]だった時の出力信号VOUT1及びVOUT2を求めてみましょう。
まず、VOUT1から求めてみます。
VOUT1を式で表すと、以下のようになりますよね?
VCC-R1IC1
hFE=∞なので、IC1≒IE1=1[mA]です。
ということは、VOUT1=VCC-R1IE1=10-1[kΩ]×1[mA]=9[V]と算出できます。
そうすると一瞬VOUT2が1[V]になりそうな気がするかもしれませんが、そうはならないのでちゃんと計算しましょう。
VOUT2も考え方は同じなので、式で表すと以下のようになります。
VOUT2=VCC-R2IC2≒VCC-R2IE2
定電流I=5[mA]に対してIE1=1[mA]なので、IE2=4[mA]だとわかります。
よって、VOUT2=VCC-R2IE2=10-1[kΩ]×4[mA]=6[V]と算出できます。
4.入力信号の差がどう結果に関わってくるのか
さて、練習問題を解いてみてこう思いませんでしたか?
『入力信号の差は条件付けされたけど、計算に使われてなくない?』と。
この練習問題の場合、すでにエミッタ電流IE1と定電流Iがわかっていたので計算に関わってこなかっただけです。
なので、一応補足説明をしておこうと思います。
差動増幅回路である図2を改めて見てください。

この回路にて、定電流源にかかる電圧V’はどうなっていると思いますか?
答えは、トランジスタQ1のエミッタ電圧VE1とトランジスタQ2のエミッタ電圧VE2の内、大きい方の電圧になります。
定電流源にトランジスタQ1のエミッタ端子とトランジスタQ2のエミッタ端子が接続されているので、当たり前ですよね。
では、入力信号VIN1が一定値で、入力信号VIN2がVIN1よりも大きかった場合について考えてみます。
エミッタ電圧は、入力信号(ベース電圧)からベース-エミッタ間電圧を差し引いた値になります。
なので、VE1=VIN1-VBE1、VE2=VIN2-VBE2と式で表せます。
ここで、エミッタ電圧の値は共通になることがわかっているので、V’=VIN1-VBE1=VIN2-VBE2という関係が成り立っていることがわかります。
その為、入力信号VIN1を一定に保っていたとしても、入力信号VIN2の影響によってV’は大きくなってしまいます。
すると、V'(上昇)=VIN1(一定)-VBE1という関係になりますので、V’が上昇した分だけベース-エミッタ間電圧VBE1が小さくなることがわかります。
ベース-エミッタ間電圧VBE1が下がると、その分ベース電流IB1も低下します。
トランジスタのベース-エミッタ間はダイオードが順方向に接続されているようなものなので、ダイオードの静特性通りに流れる電流が減少するんです。
そうすると、ベース電流IB1が減少した分だけ出力電流であるコレクタ電流IC1(電流増幅率hFE×ベース電流IB1)も減少するわけです。
出力電流IC1が減少すると抵抗R1での電圧降下が減少するので、出力信号VOUT1は増加します。
トランジスタQ2側ではどうなっているかというと、トランジスタQ1とは逆の動きをしています。
コレクタ電流IC1が減少しているのでエミッタ電流IE1も減少し、定電流源が存在する関係上エミッタ電流IE2は増加することがわかります。
同様にコレクタ電流IC2も増加していますので、抵抗R2での電圧降下が増加します。
結果、出力信号VOUT2は小さくなります。
つまり、入力信号に電位差を持たせると、入力信号が大きい方のトランジスタ側の出力信号は小さくなり、入力信号が小さい方はトランジスタ側の出力信号は大きくなります。
以上、「差動増幅回路」についての説明でした。




