今回は、「論理回路の考え方」についての説明です。
1.実際の回路と論理式の関係
論理回路における基本的な演算回路は以下のような種類があります。
- AND回路
- OR回路
- NOT回路
- NAND回路
- NOR回路
- XOR回路
これらの演算回路の説明をする際に、実際の回路構成を例に挙げていました。
今回は、例を用いて実際の回路と論理式の関係をもう少し詳しく見ていこうと思います。
2.例①直列回路
まずは図1のような単純な直列回路について見ていきます。
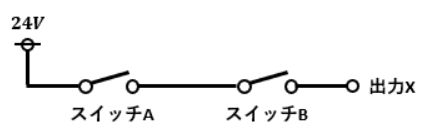
スイッチA及びスイッチBのON/OFF状態に対して、出力Xの先に繋ぐ負荷に電流が流れるかどうかを論理式で表していきます。
各スイッチの状態における論理式は以下のように表します。
| ON | OFF | |
|---|---|---|
| スイッチA | A | A |
| スイッチB | B | B |
スイッチON/OFFの組み合わせは以下の4パターンです。
スイッチAがOFF、スイッチBがOFF
→A・B
スイッチAがOFF、スイッチBがON
→A・B
スイッチAがON、スイッチBがOFF
→A・B
スイッチAがON、スイッチBがON
→A・B
この4パターンの内、回路が繋がるのはA・Bの時のみです。
つまり、この回路構成において出力Xに24Vを供給するには、X=A・Bである必要があると言えます。
このような論理演算がAND回路に当たるわけです。
A・B以外の論理式では出力Xに電流が流れませんからね。
3.例②並列回路
次は図2のような単純な並列回路について見ていきます。
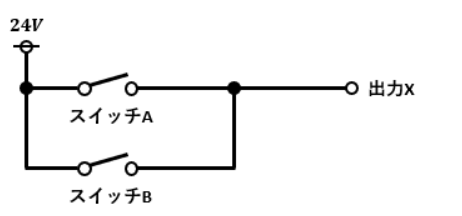
スイッチA及びスイッチBのON/OFF状態に対して、出力Xの先に繋ぐ負荷に電流が流れるかどうかを論理式で表していきます。
各スイッチの状態における論理式は以下のように表します。
| ON | OFF | |
|---|---|---|
| スイッチA | A | A |
| スイッチB | B | B |
スイッチON/OFFの組み合わせは以下の4パターンです。
スイッチAがOFF、スイッチBがOFF
→A・B
スイッチAがOFF、スイッチBがON
→A・B
スイッチAがON、スイッチBがOFF
→A・B
スイッチAがON、スイッチBがON
→A・B
この4パターンの内、回路が繋がるのはスイッチA・スイッチB共にOFFであるA・Bの時以外です。
つまり、この回路構成において出力Xに24Vを供給するには、X=A・B、X=A・B、X=A・Bの何れかである必要があると言えます。
このような論理演算がOR回路に当たるわけです。
A・B以外の論理式では出力Xに電流が流れますからね。
ここまでは復習です。
4.例③直列回路と並列回路が合わさった場合
次は図3のような直列回路と並列回路が合わさった場合について見ていきます。
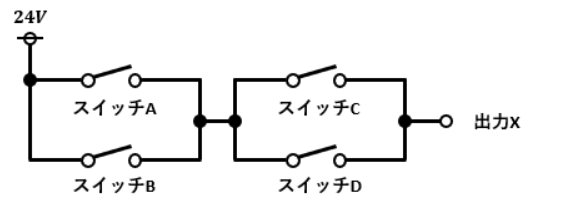
スイッチA・スイッチB・スイッチC・スイッチDのON/OFF状態に対して、出力Xの先に繋ぐ負荷に電流が流れるかどうかを論理式で表していきます。
各スイッチの状態における論理式は以下のように表します。
| ON | OFF | |
|---|---|---|
| スイッチA | A | A |
| スイッチB | B | B |
| スイッチC | C | C |
| スイッチD | D | D |
スイッチAとスイッチB、スイッチCとスイッチDはそれぞれ並列に繋がっているのでOR回路になっています。
なので、論理式はA+BとC+Dになります。
このOR回路が直列に繋がっているので、回路全体の論理式は(A+B)・(C+D)と表せます。
この論理式は全スイッチがONの場合の論理式です。
仮に、スイッチAとスイッチCがON、スイッチBとスイッチDがOFFだったとすると、論理式は(A+B)・(C+D)となります。
この論理式の形だと負荷Xに電流が流れるか判断するのは難しいですが、式を変形させると判断が可能になります。
(A+B)・(C+D)
=(A+B)・C+(A+B)・D
=AC+BC+AD+BD
※分配則を使用。
ここで図3を改めて見てみましょう。
そもそもこの回路の経路を考えると、スイッチA-スイッチC、スイッチA-スイッチD、スイッチB-スイッチC、スイッチB-スイッチCの4パターンしかないですよね?
その為、回路全体を表す論理式の中にAC、AD、BC、BDの何れかが含まれていれば回路に電流は流れます。
つまり、X=AC+AD+BC+BDが回路に電流が流れる条件だと言えます。
※ (A+B)・(C+D)に分配則を適用したらAC+AD+BC+BDになる。
よって、(A+B)・(C+D)の場合はACが存在するので、回路に電流が流れることがわかります。
以上、「論理回路の考え方」についての説明でした。




