今回は、「R－L－C直並列回路の定常状態の考え方」についての説明です。
１．R－L－C直並列回路の定常状態の考え方
「過渡現象と時定数」の説明をした際に、R－L回路とR－C回路の特徴が以下のようになると説明をしました。
電源印加時はLを開放して考え、一定時間経過後はLを短絡して考える。
時定数Tは、T=L/Rで表される。
電源印加時はCを短絡して考え、一定時間経過後はCを開放して考える。
時定数Tは、T=CRで表される。
これらの関係を踏まえた上で、以下の図１の回路を見てください。
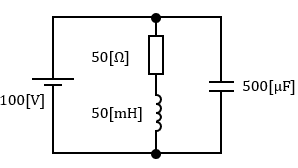
この回路にて、『定常状態の時のコイルとコンデンサのエネルギーの総和を求めよ』という問題を振られた場合、咄嗟に解法がわかりそうでしょうか？
おそらくよくわからないのではないかと思います。
なのですが、実はこの問題、最初に示したR－L回路とR－C回路の特徴を知っていれば普通に解けます。
言葉ではわかっているつもりでも、それを応用できるかはまた別問題なんですよね。
ということで、今回はこの回路を使ってR－L－C直並列回路の定常状態の考え方について説明していきます。
２．実際の考え方
根本的なところなのですけど、“定常状態”という言い方がまずややこしいんですよね。
下手したら教科書や参考書には定常状態とは書いてありませんから。
「一定時間経過後に一定値に収まる現象」とか「過渡現象」という表記なら見たことがあるのではないでしょうか？
これ、定常状態のことです。
“定常”とは、“常に一定の状態を保つこと”です。
コイルの場合、電流が流れるとその流れを妨げるような起電力を発生させますが、そのまま一定の電流を流していると電流を妨げなくなって電流値が一定になります。
コンデンサの場合、電流が流れると充電を開始し、充電が完了すると電流が流れないという一定の状態になります。
つまり、図１の回路が定常状態ということは、コイルが短絡、コンデンサが開放になった状態を指します。
するとどうなるかと言うと、直流電源に抵抗が一つ繋がっただけの回路と見なせるわけです。
なので、抵抗Rに流れる電流IRは、オームの法則からIR=100/50=2[A]だとわかります。
ということは、このR－L－C直並列回路において、コイルには2[A]の電流、コンデンサには100[V]の電圧が掛かっていることになります。
ここまでわかれば後は簡単です。
コイルの蓄える磁気エネルギーはLI2/2、コンデンサの蓄える静電エネルギーはCV2/2で表されるので、50×10-3×22/2+500×10-6×1002/2=2.6[J]が定常状態の時のコイルとコンデンサのエネルギーの総和となります。
コイルの蓄える磁気エネルギーとコンデンサの蓄える静電エネルギーについては、以下の記事を参考にしてください。
定常状態とは一体何なのかしっかり理解していればそんなに難しくない問題だったんですよ。
逆に言うと、書物で目を通しただけだとわからない人の方が多いと思われます。
以上、「R－L－C直並列回路の定常状態の考え方」についての説明でした。
