今回は、「磁界と電流の関係」についての説明です。
1.ポイント
導線(導体)に電流が流れると、導線の周りには円形状の磁界が発生する。
電流の流れる向きと円形状の磁界の向きの関係を紐づける法則を右ねじの法則と呼ぶ。
2.右ねじの法則とは?
導線に電流が流れると、導線の周りには円形状の磁界が発生します。
このことを磁気作用と呼びます。
その為、電気回路に方位指針を近づけると磁針に影響が出ます。
電流の流れる向きと円形状の磁界の向きの関係を紐づける法則が右ねじの法則です。
アンペアの右ねじの法則とも呼びます。
電流と磁界の関係をねじの進む方向とねじの回転する方向に置き換えた考え方です。
では、どういった法則なのか説明していきます。
まず、右手でサムズアップして下さい。⇒⇒👍
この時、親指が指す方向が電流の向き、親指以外の指が指す方向が磁界の向きです。
ねじに置き換えると、ねじの進行方向が電流の向き、ねじの回転方向が磁界の向きです。
つまり、直線導体の場合の電流と磁界の向きの関係は図1のようになります。
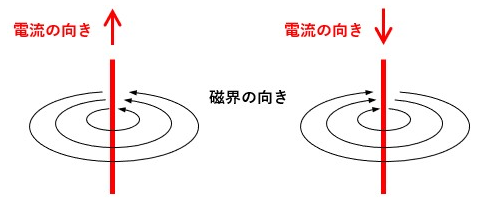
ちなみに、真上から見た時の電流が流れる方向は図2のように表します。
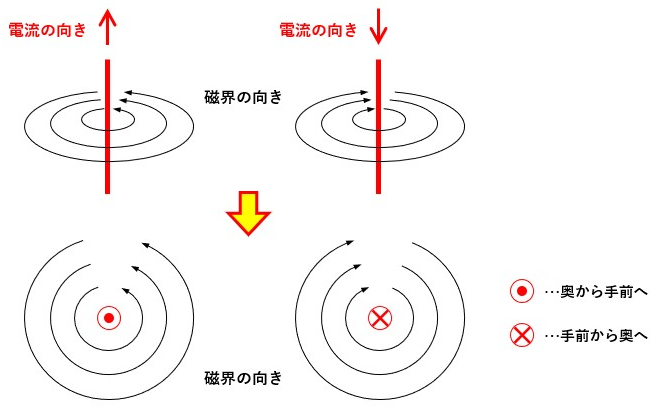
プラスドライバーで回すねじの形状がモチーフですかね?
円形導体に電流が流れている場合も考え方は同じで、任意の点で右ねじの法則を当て嵌めます。
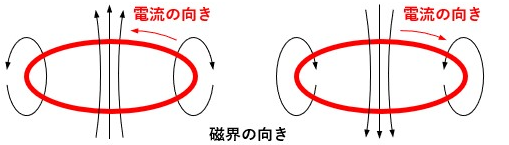
つまり、円形導体であるコイルの磁界は図3のように発生していると言えます。
コイルの場合、コイルの中心に発生している磁界は真っ直ぐになります。
このコイルの半径をr[m]、コイルに流れる電流をI[A]とすると、コイルの円の中心に発生する磁界の強さH[A/m]は次のように表せます。
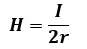
つまり、円形コイルの中心磁界の強さH[A/m]は、コイルに流れる電流をコイルの直径で割った値になります。
なお、コイルの中心磁界はコイルの巻数Nに比例して強まります。
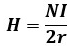
3.アンペアの周回路の法則とは?
電流が流れると磁気作用により磁界が発生します。
電流が流れることにより発生した磁界中で、磁界の強さH[A/m]が等しい箇所を辿ると1周して円状になります。
この円状になっている道のことを磁路と呼びます。
磁路の長さl[m]と磁界の強さH[A/m]の積が電流I[A]になります。
この関係をアンペアの周回路の法則と呼びます。
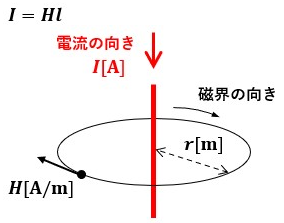
図4のように直線導体(無限長)に電流I[A]が流れていて、導体の中心からr[m]離れた位置に磁界の強さH[A/m]が等しい箇所を辿った磁路(円)が存在するとします。
この磁路の長さl[m]は、直径×π=2πrです。
その為、アンペアの周回路の法則より、H×2πr=Iとなります。
よって、この場合の磁界の強さH[A/m]は以下のように表せます。
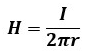
磁界の強さの単位は[A/m]なので、それと連動させると覚えやすいです。
4.まとめ
直線導体に電流I[A]が流れた時、磁界の強さH[A/m]は電流I[A]を磁路の長さ[m]で割った値となる。
円形導体に電流I[A]が流れた時、円の中心磁界の強さH[A/m]は電流I[A]を円の直径[m]で割った値となる。
以上、「磁界と電流の関係」についての説明でした。




