今回は、「組み合わせ論理回路の考え方」についての説明です。
1.実際の回路と論理式の関係
論理回路における基本的な演算回路は以下のような種類があります。
- AND回路
- OR回路
- NOT回路
- NAND回路
- NOR回路
- XOR回路
これらの論理回路(論理ゲート)を複数個組み合わせて構成する論理回路のことを組み合わせ論理回路と呼びます。
今回は、論理式を論理ゲートの組み合わせで表現する方法を例を用いて説明していきます。
2.例①
X=AB+CDという論理式を論理ゲートで表してみましょう。
ABはA・B、つまり論理変数Aと論理変数BのAND回路です。
CDも同様にAND回路ですね。
X=AB+CDなので、後はABとCDをORゲートで繋ぐだけです。
以上より、X=AB+CDという論理式は以下のような論理回路で表せます。
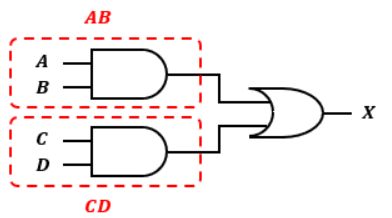
3.例②
X=AB+CDという論理式を論理ゲートで表してみましょう。
ABはA・B、つまりAとBのAND回路です。
CDも同様にAND回路ですね。
この関係自体は例①と変わらないのですが、今度はAがAに反転しています。
なので、AとBのAND回路を組む前にAをNOT回路に通す必要があります。
X=AB+CDなので、後はABとCDをORゲートで繋ぐだけです。
以上より、X=AB+CDという論理式は以下のような論理回路で表せます。
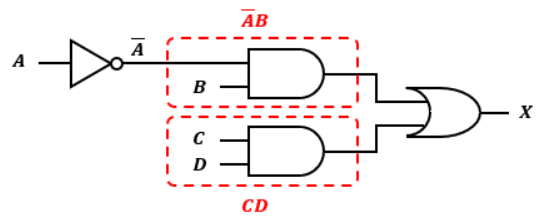
接続するゲートの順番には注意が必要です。
4.例③
X=A(B+C)+BCDという論理式を論理ゲートで表してみましょう。
一気に見た目が複雑になりましたが、考え方はこれまでと同じです。
まず、全体を見るとA(B+C)とBCDのOR回路になっていますよね?
なので、一番右は以下のようになります。
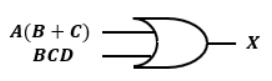
上側のゲートにA(B+C)、下側のゲートにBCDを入力とすれば良いわけです。
なので、図4のようになります。
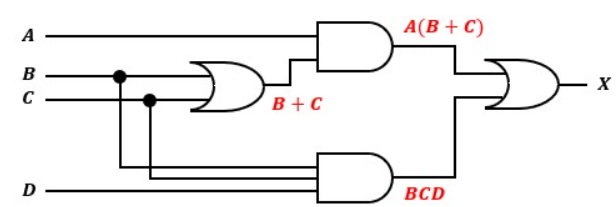
※ BCDのような3入力のAND回路なんかも存在します。
論理式が複雑になっても基本的な考え方は何も変わらないので、階層分けをして順番に考えていきましょう。
以上、「組み合わせ論理回路の考え方」についての説明でした。




