今回は、「交換則と分配則」についての説明です。
1.ポイント
A・B=B・A、A+B=B+Aの関係のこと。
A+(B・C)=(A+B)・(A+C)、A・(B+C)=(A・B)+(A・C)の関係のこと。
2.公理と定理
論理回路には公理と定理が存在します。
公理…理由なく正しいこと。
定理…公理から導き出された正しいこと。
つまり、前提知識・基礎知識みたいなヤツです。
公理と定理は結構な数があり、本当に基本的過ぎて特に覚えるように意識する必要の無いものも存在します。
この公理の中に交換則と分配則というものがあり、この考え方は地味に重要になります。
なので、本記事ではその説明をしていこうと思います。
3.交換則
「真偽と真理値表」の説明で、論理積(AND)・論理和(OR)・否定(NOT)は以下のような記号で表されると述べました。
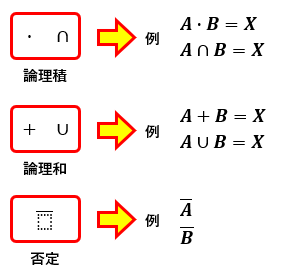
この論理積及び論理和において、以下の関係が成り立っています。
A・B=B・A
A+B=B+A
これを交換則と呼びます。
論理変数Aと論理変数Bの並びを交換しても問題は無いという関係です。
当たり前のように感じるかもしれませんが、A・BはA×Bとは意味が異なるのでそんな単純でも無かったりします。
実際、後で説明する分配則で特に顕著な変化が出ます。
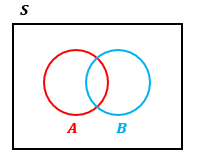
集合Sの中に論理変数Aと論理変数Bが存在します。
A及びBが“1”なら円の中、“0”なら円の外(集合S内に限る)を指し示します。
※ ちなみに、集合Sの中にA・B及びA+Bが含まれているというのも公理です。
A・Bの場合、AとB両方の条件を満たしている状態を指すので、図3の斜線部分を示していることになります。
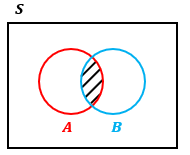
図3を見てわかる通り、A・BもB・AもAとBの共通している箇所を示しているのでA・B=B・Aが成り立っていることがわかります。
A+Bの場合、AまたはBの条件を満たしている状態を指すので、図4の斜線部分を示していることになります。
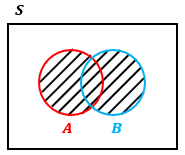
図4を見てわかる通り、A+BもB+AもAもしくはBという範囲を示しているのでA+B=B+Aが成り立っていることがわかります。
4.分配則
問題の分配則についてです。
分配則とは、以下の関係を指しています。
A+(B・C)=(A+B)・(A+C)
A・(B+C)=(A・B)+(A・C)
「・」を「×」に置き換えて考えてしまうとこうはならないですよね。
今やっているのはあくまで論理演算だということを忘れないようにしましょう。
分配則の関係は実際に図示して比較すると正しいことがわかります。
逆に言うと、図示しないと覚えていない限り間違えます。
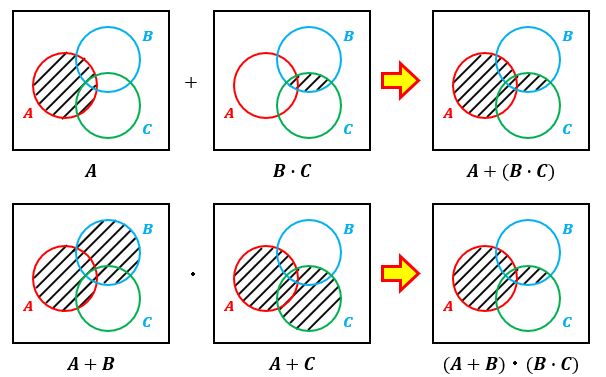
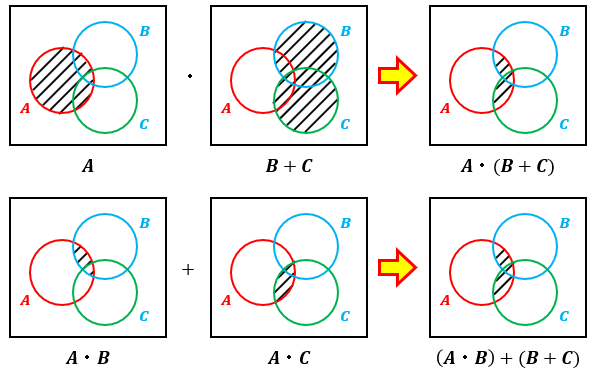
忘れた場合は面倒くさがらずに図示するようにしましょうね。
以上、「交換則と分配則」についての説明でした。




