【基礎から学ぶコンデンサ】コンデンサからなる直並列回路の端子電圧の考え方

“コンデンサ”という部品は、電気製品なら必須レベルで多用されています。
電気を蓄えたり放出したり、ノイズ成分を吸収したり、何かと便利だからです。
本記事では、そんなコンデンサという部品についての知識をわかりやすくまとめてみました。

今回は、「コンデンサからなる直並列回路の端子電圧の考え方」についての説明です。

コンデンサからなる直並列回路の端子電圧を求めるポイント

電源に直列にコンデンサが繋がっている場合、電荷は等しくなる。

図1のようなコンデンサからなる直並列回路があります。
この時、各コンデンサの端子電圧V₁、V₂、V₃、V₄を電源電圧Vで表すとどうなるか求めてみます。

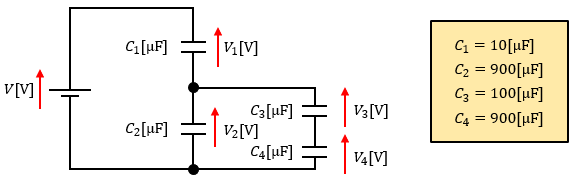
「コンデンサの合成静電容量」の説明で、コンデンサを直列接続すると各コンデンサに蓄えられる電荷が等しくなると説明しました。
今回はこの関係が重要になってきます。

まず、並列回路になっている部分の合成静電容量C₂₃₄を求めて、図2のような構成にします。

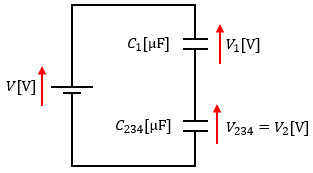
計算すると、C₂₃₄=C₂+C₃C₄/(C₃+C₄)=990[μF]になります。
これで、電源VにC₁とC₂₃₄が直列接続された単純な回路になりました。

ここで今回のポイントが活きてきます。
C₁とC₂₃₄に蓄えられる電荷は等しくなるのです。
具体的には、Q=CVの関係から、C₁V₁=C₂₃₄V₂、10V₁=990V₂になります。
つまり、V1：V2=990：10になります。
よって、V₁及びV₂は以下のようになります。

V₁=V×990÷(10+990)=99V/100

V₂=V×10÷(10+990)=V/100

要するに、電源－コンデンサ－コンデンサと直列に繋がっていたら、コンデンサの静電容量で逆比例配分してあげれば各端子電圧は求められるということです。

V₂=V/100なので、C₃とC₄の直列回路にかかる電圧もV/100になっています。
なので、図3のように電源(V/100)－コンデンサ(C3=100[μF])－コンデンサ(C4=900[μF])が直列に繋がっていると見なせます。

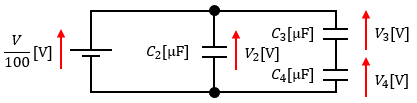
よって、先程同様に逆比例配分してあげればコンデンサの端子電圧を求めることができます。

V₃=(V/100)×900÷(100+900)=9V/1000

V₄=(V/100)×100÷(100+900)=V/1000

コンデンサの電荷を蓄える仕組みをしっかりと理解していれば初見でも解くのは難しくはないので、躓いた方はこの機に復習してみるといいかもです。

以上、「コンデンサからなる直並列回路の端子電圧の考え方」についての説明でした。