今回は、「コンデンサ回路の電圧と電流の時間的変化」についての説明です。
1.ポイント
※ t秒間にQ[C]の電荷が移動したときの電流をi[A]とする。
i=dQ/dt
つまり、1秒間に1Cの電荷が移動したら1Aの電流が流れる。
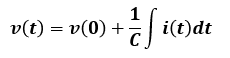
2.コンデンサ回路の電圧と電流の時間的変化
電荷と電流の関係は以下のようになっていました。
【単位時間当たりの電荷の変化量が電流】
i(t)=dQ/dt
※ t秒間にQ[C]の電荷が移動したときの電流をi(t)[A]とする。
Q=CVを代入すると、i(t)=dCv(t)/dtとなります。
この式を変形すると以下のようになります。
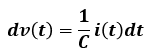
この式を積分することでコンデンサ回路の電圧と電流の時間的変化の式を求めることが可能です。
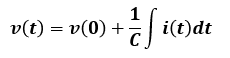
3.練習問題
関係式だけ見ても中々理解はできないと思いますので、例題を見ながら実際にどうなるのかを考えてみましょう。
静電容量1[F]、初期電荷0[C]のコンデンサに以下のように時間変化する電流源を接続してあるとします。
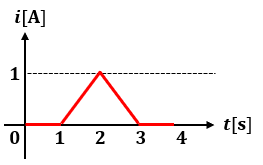
区間ごとにコンデンサにかかる電圧v(t)の時間的変化を求めてみます。
《t=0~1[s]の区間》
初期電荷が0[C]なので、v(0)=Q/C=0[V]です。
その為、v(t)=0+1×∫i(t)dt=∫i(t)dtと表せます。
i(t)=0なので、積分しても0です。
よって、t=0~1[s]の区間は電圧が0[V]のまま変化しません。
《t=1~2[s]の区間》
t=1~2[s]の区間は、t=1[s]時点を0点だと仮定すると電流i(t)=tという一次関数で表せます。
また、t=1[s]時点では電圧が0[V]だとわかっています。
つまり、v(1)=0[V]です。
その為、v(t)=v(1)+∫i(t)dt=∫tdt=t2/2と表せます。
今はt=1~2[s]の区間について考えていますが、この積分の式における0点はt=1[s]の時ですよね?
なので、積分の範囲を0~t-1[s]と考える必要があります。
つまり、以下のように考える必要があります。
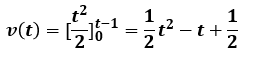
この式から、t=1[s]の時はv(1)=0[V]、t=2[s]の時はv(2)=2-2+0.5=0.5[V]とわかります。
よって、t=1~2[s]の区間はt=1[s]の時は0[V]、t=2[s]の時は0.5[V]、t=1~2[s]の間はv(t)の式に従って変化します。
《t=2~3[s]の区間》
t=2~3[s]の区間は、t=2[s]時点を0点だと仮定すると電流i(t)=1-tという一次関数で表せます。
また、t=2[s]時点では電圧が0.5[V]だとわかっています。
つまり、v(2)=0.5[V]です。
その為、v(t)=v(2)+∫i(t)dt=0.5+∫(1-t)dt=0.5+t-t2/2と表せます。
今はt=2~3[s]の区間について考えていますが、この積分の式における0点はt=2[s]の時ですよね?
なので、積分の範囲を0~t-2[s]と考える必要があります。
つまり、以下のように考える必要があります。
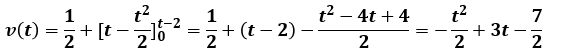
この式から、t=2[s]の時はv(2)=0.5[V]、t=3[s]の時はv(3)=-4.5+9-3.5=1.0[V]とわかります。
よって、t=2~3[s]の区間はt=2[s]の時は0.5[V]、t=3[s]の時は1.0[V]、t=2~3[s]の間はv(t)の式に従って変化します。
《t=3~4[s]の区間》
v(3)=1.0[V]だとわかっています。
その為、v(t)=1+∫i(t)dtと表せます。
i(t)=0なので、積分しても0です。
よって、t=3~4[s]の区間は電圧が1.0[V]のまま変化しません。
上記を踏まえると、コンデンサにかかる電圧v(t)は図2のように変化することがわかります。
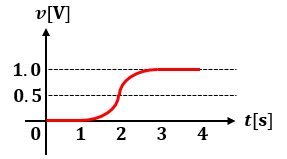
順を追って考えていけばそこまで難しくはないんですよ。
そこまで…ね。
以上、「コンデンサ回路の電圧と電流の時間的変化」についての説明でした。




