【基礎から学ぶ電気回路】キルヒホッフの第一法則と第二法則

電気電子系は難しいイメージを持たれがちですが、基本から順番に抑えていけばそれほど難しいものではありません。
どんな分野にも言えることですが、最初はよくわからないものですから。
本記事では、電気初心者の方でもわかりやすいように、電気回路を理解するための基本中の基本から順を追って解説していきます。
まずは、直流回路についてです。

今回は、「キルヒホッフの法則」についての説明です。

１．キルヒホッフの法則

「キルヒホッフの法則」はドイツの物理学者グスタフ・キルヒホフが発見しました。
キルヒホッフさんではなく、キルヒホフさんです。

「キルヒホッフの法則」には、第1法則と第2法則があります。
それぞれの説明は以下の通りです。

キルヒホッフの第1法則

電気回路の分岐点・合流点に流入する電流の総和＝流出する電流の総和

言葉だけだとイメージが付きづらいので、図を使って考えるとすんなり理解できます。

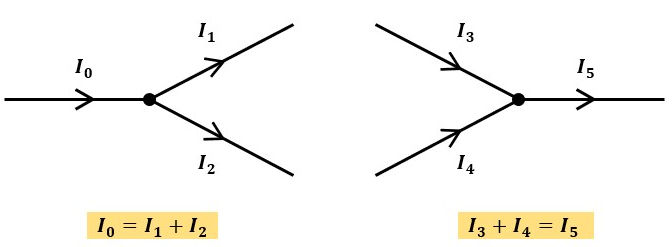
図1左側は電流I₀が分岐点に流入し、I₁とI₂として流出した場合の電流の関係です。
図1右側は電流I₃とI₄が合流点に流入し、I₅として流出した場合の電流の関係です。
ある物体に電流が流れ込んだ時、その物体を通過して出てくる電流量は流入した分と変わらないということです。

『あれ、それだけ？』と思うかもしれません。

はい。それだけです。

それだけが重要なんです。

ちなみに、第1法則の“電流は途中でなくなることはない”という特徴のことをKCL[Kirchhoff’s Current Law]と呼んでいて、小難しい文献ではよく見かけます。

キルヒホッフの第2法則

閉回路内の起電力の和＝電圧降下の和

閉回路とは、電流が流れる状態になっている電気回路のことです。
電圧降下とは、抵抗に電流が流れた際に発生する電圧のことです。

相変わらず言葉だけではわかりにくいので、図を使って説明していきます。
例えば、次のような電気回路があるとします。

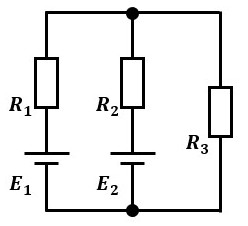
この電気回路から、図3のように赤矢印部と青矢印部を抜き出して考えます。

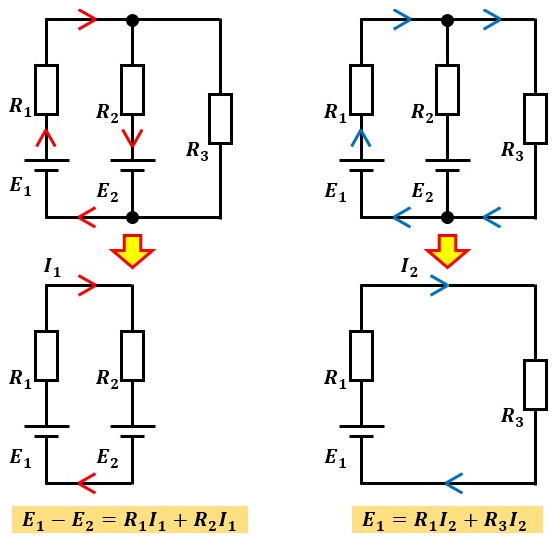
それぞれ抜き出した回路についてですが、いずれも起電力があり、抵抗が繋がっているので何かしら電流が流れる電気回路になっていますよね？
つまり、閉回路になっているので、キルヒホッフの第2法則が適用できます。

キルヒホッフの第2法則に則った数式が図の下に書いてあります。
左辺が起電力の和、右辺が電圧降下の和です。

赤矢印部のように起電力が2つ以上ある場合は注意が必要です。
電流I₁の向きを図のように定めている時、起電力E₁から流れる電流の向きと電流I₁の向きは同じですが、起電力E₂から流れる電流の向きと電流I₁の向きは逆です。
その為、左辺の起電力の和がE₁＋E₂ではなく、E₁－E₂になります。