【基礎から学ぶ電気回路】 過渡現象と時定数の考え方

今回は、「過渡現象と時定数」についての説明です。

１．ポイント

ある状態から時間経過に従って変化し、一定時間経過後に一定値に収まる(定常状態になる)現象のことを過渡現象と呼びます。
時間経過で状態が落ち着く(澄み渡る)現象とでも覚えてください。
電気回路では、コイルやコンデンサが繋がっていると過渡現象が発生します。

コンデンサを例に考えてみますね。

コンデンサは電気を蓄えたり放出したりできます。
空のコンデンサに電気を加えれば充電され、充電済みのコンデンサに負荷が繋がれば放電されます。
なので、充電されたコンデンサに負荷を繋いだ場合、状態は以下のように変化します。

これが過渡現象です。
一番最初の過渡現象の説明と読み比べてみれば同じことを言っているのがわかるかと思います。

具体的にどのような状態になるのかを説明していきます。

２．R－L回路の過渡現象・時定数

R－L直列回路にスイッチSが付いています。
この回路でスイッチSを接点aと繋いだ直後からの電流Iの変化は以下のグラフのようになります。

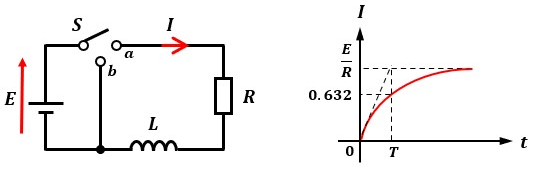
ある状態から時間経過に従って変化し、一定時間経過後に一定値に収まる(定常状態になる)現象のことを過渡現象と呼び、この時に流れる電流を過渡電流と呼びます。

また、一定値(定常値)に落ち着いた状態の電流を定常電流と呼びます。

回路に流れる電流Iは、電源印加時はLを開放して考え、一定時間経過後はLを短絡して考えます。

コイルは電流の流れを妨げる向きに起電力(逆起電力と呼ぶ)を発生させます。
その為、電流の増加を妨げようとしてグラフのようなカーブを描きます。

電流はグラフから見てわかる通り、時間経過で定常値であるE/Rに近づきます。
この過程で、最終値の63.2%に達するまでにかかる時間のことを時定数と呼びます。
時定数は量記号T、単位は[s]です。
時定数は、任意の時間tにおいて接線(その地点での電流の増加率に値する)を引いた時に定常値E/R[A]に達するまでの時間に等しくなります。

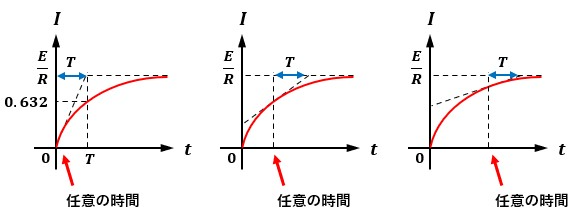
R－L直列回路の時定数Tは、T=L/Rとなります。

定常状態になった後、スイッチSを接点aから接点bに瞬時に切り換えた時、電流Iの変化は以下のグラフのようになります。

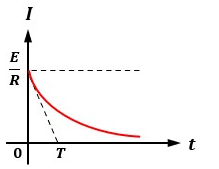
接点bに切り換えると電源が切り離される為、通常なら電流は流れなくなります。
ただ、コイルは電流の流れを妨げる向きに起電力(逆起電力と呼ぶ)を発生させるので、コイルに蓄えられているエネルギーを消費して電流の減少を妨げようとします。
その為、グラフのようなカーブを描きます。

また、時定数の考え方は電源除去時にも反映され、任意の時間tにおいて接線(その地点での電流の増加率に値する)を引いた時に0[A]に達するまでの時間に等しくなります。

３．R－C回路の過渡現象・時定数

R－C直列回路にスイッチSが付いています。
この回路でスイッチSを接点aと繋いだ直後からのコンデンサの端子電圧V_Cの変化は以下のグラフのようになります。

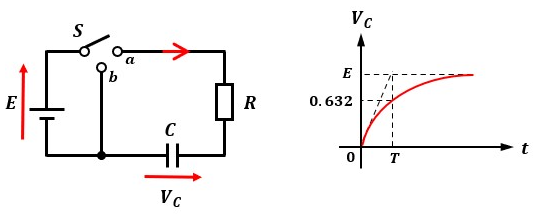
ある状態から時間経過に従って変化し、一定時間経過後に一定値に収まる(定常状態になる)現象のことを過渡現象と呼び、この時の電圧を過渡電圧と呼びます。
また、一定値(定常値)に落ち着いた状態の電圧を定常電圧と呼びます。

コンデンサの端子電圧V_Cは、電源印加時はCを短絡して考え、一定時間経過後はCを開放して考えます。

コンデンサに電圧をかけると電荷が蓄えられ、充電が開始されます。
充電が完了するとコンデンサの端子電圧V_Cは電源電圧Eと同じになります。
その為、充電の過程でグラフのようなカーブを描きます。

また、時定数の考え方はR－C直列回路にも反映されます。
R－C直列回路の時定数Tは、T=CRとなります。

定常状態になった後、スイッチSを接点aから接点bに瞬時に切り換えた時、コンデンサの端子電圧V_Cの変化は以下のグラフのようになります。

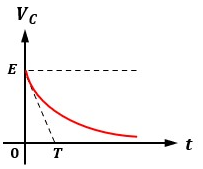
接点bに切り換えると電源が切り離される為、コンデンサの端子電圧V_Cと抵抗Rが繋がった状態になり、コンデンサが放電を開始することで時間の経過に伴いコンデンサの端子電圧V_Cは徐々に減少し、最終的に0[V]になります。
その為、放電の過程でグラフのようなカーブを描きます。

以上、「過渡現象と時定数」についての説明でした。

---