今回は、「カルノー図を用いた論理式の表し方」についての説明です。
1.ポイント
論理変数を縦軸と横軸に割り当てて、全組み合わせを書き並べた図のこと。
論理式の該当箇所に“1”と表記する。
2.カルノー図とは?
論理変数の全組み合わせを網羅した表を真理値表と呼びました。
論理積であるX=A・Bを例にすると、真理値表は以下のようになります。
| A | B | X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
真は“1”、偽は“0”に対応するわけですが、論理変数Aに焦点を当てた場合、“1”の時は“A”、“0”の時は“A”と表します。
つまり、Xには[A・B]、[A・B]、[A・B]、[A・B]の4種類の組み合わせがあることがわかります。
この関係は、以下のように表すことが可能です。
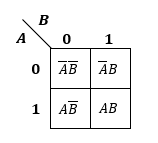
このように、論理変数を縦軸と横軸に割り当てて、全組み合わせを書き並べた図のことをカルノー図と呼びます。
3.カルノー図を用いた論理式の表し方
先程の例ではX=A・BやX=A+Bといった論理変数が少ない(2変数しかない)場合のカルノー図について説明しました。
では、論理変数が増えた場合はどうなると思いますか?
答えは、論理変数が増えても普通にカルノー図で表示可能です。
例えば、4変数なら以下のようになります。
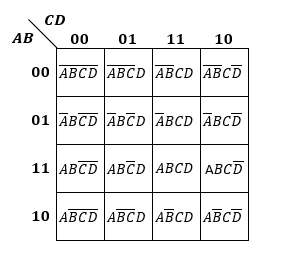
※ カルノー図を描く際には注意点があり、隣り合うマス目の間では1つの変数しか変化しません。
ここで、X=ABCD+ABCD+ABCDという論理式があったとします。
この場合、カルノー図では以下のように表します。
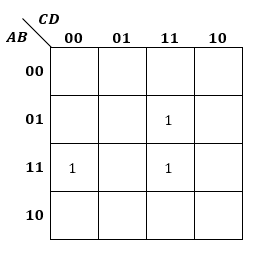
該当する箇所に“1”と表記するようにします。
では、X=ABC+ADという論理式ではどうなるでしょうか?
この場合、ABCはABCDとABCDの両方を示していることになります。
ADも同様に考えると、以下のようになります。
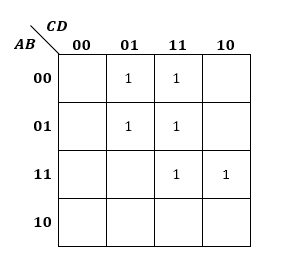
4変数なのに論理式には4つ変数が入っていない場合なども存在しますので注意しましょうね。
ちなみに、論理変数6つになった場合は以下のようになります。
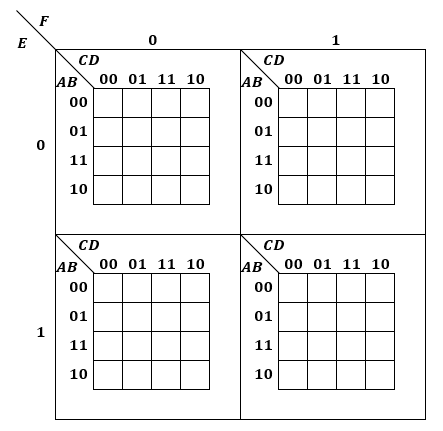
このように、論理変数が多くてもカルノー図は一応描けますが、どんどん複雑になって実用性は皆無になっていきます。
以上、「カルノー図を用いた論理式の表し方」についての説明でした。




