今回は、「自己インダクタンス」についての説明です。
1.ポイント
自己誘導作用時のコイルの性質を表す比例定数のこと。
自己インダクタンスは磁束鎖交数をコイルに流れる電流で割った値となる。
※磁束鎖交数=コイルの巻数×磁束
環状コイルの自己インダクタンスは、コイルの巻数の2乗に比例し、磁気抵抗に反比例する。
2.自己インダクタンスとは?
コイルと鎖交する磁束を変化させるとコイルに起電力が発生し、電流が流れるという現象を電磁誘導と呼びました。
これに対し、コイルに流れる電流を変化させるとコイルと鎖交する磁束が変化し、コイルに起電力を誘起するという現象を自己誘導作用と呼びます。
この時誘起する起電力を自己誘導起電力と言います。
例えば、コイルに電源を印加している回路があり、この回路の電源を切ると電流は減少します。
その際、電流の減少を妨げる向きにコイルが自己誘電起電力を誘起します。
コイルに流れる電流がΔt[s]の間にΔI[A]だけ変化したとします。
Δtは電流変化時の経過時間、ΔIは電流の変化量を表しています。
この時、コイルに誘起される自己誘導起電力e[V]は以下のようになります。
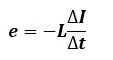
Lは自己誘導作用時のコイルの性質を表す比例定数で、自己インダクタンスと言います。
単位は[H]です。
電流の減少を妨げる向きにコイルが自己誘電起電力を誘起する為、符号は-(マイナス)になります。
電流の変化の方向と向きが逆の起電力を誘起する為、この起電力のことを逆起電力と呼びます。
電磁誘導に関するファラデーの法則より、電磁誘導により発生する起電力の大きさe[V]は、コイルと鎖交する磁束の変化量に比例することがわかっています。
※巻数N[回]のコイルに鎖交する磁束がΔt[s]の間にΔΦ[Wb]だけ変化した場合の起電力。
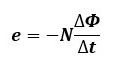
自己誘導作用の関係式と電磁誘導作用の関係式を照らし合わせて式を整理します。
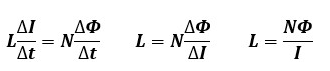
ΔΦ[Wb]とΔI[A]はどちらもΔt[s]当たりの変化量なので比例します。
その為、最終式ではΔを取っています。
最終式の分子であるコイルの巻数N[回]と磁束Φ[Wb]の積NΦのことを磁束鎖交数と呼びます。
つまり、自己インダクタンスは磁束鎖交数をコイルに流れる電流で割った値となります。
この関係から、磁束鎖交数は電流に比例することがわかります。
NΦ=LI
また、I=1[A]の時は自己インダクタンスL=磁束鎖交数NΦとなります。
3.環状コイルの自己インダクタンス
環状コイルの自己インダクタンスについて考えます。
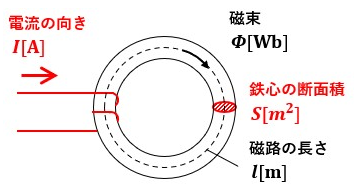
図1のようにコイルの巻数N[回]の環状コイルがあります。
コイルに電流I[A]が流れて鉄心内を磁束Φ[Wb]が通っています。
磁束密度はB[T]、磁路の長さはl[m]、鉄心の断面積はS[m2]です。
この環状コイルの自己インダクタンスについて考えます。
自己インダクタンスL=NΦ/Iでしたので、この式を変形していきます。

以上より、環状コイルの自己インダクタンスはコイルの巻数N[回]の2乗に比例し、磁気抵抗Rm[A/Wb]に反比例することがわかります。
ここまで出てきた関係式をしっかり覚えていないと導き出せませんので、記憶に定着させるために自分で式を変形してみるのも良いと思います。
※少なくとも私の過去の記事のどこかに載っている関係式を使用しています。
以上、「自己インダクタンス」についての説明でした。




