今回は、「インピーダンスとアドミタンス」についての説明です。
1.初めに
電気系の学科に進むと、インピーダンスという概念が出てきます。
インピーダンスという用語は頻繁に登場するので覚えている人は多いでしょう。
では、アドミタンス・コンダクタンス・リアクタンス・サセプタンスってわかりますか?
これらの用語は、全てインピーダンスと何らかの関係があります。
ただ、全部「○○ンス」という形になっているので、結構どれがどれなのかわからなくなるんですよ。
ということで、今回はこれらの用語の意味をまとめてみました。
2.インピーダンスとは?
インピーダンス[impedance]とは、交流回路における電流の流れにくさのことです。
要するに、直流回路における抵抗みたいなものです。
量記号はZ、単位は[Ω]です。
インピーダンスは、抵抗だけでなく、コイルやコンデンサといった周波数によって抵抗値が変化する素子についても考慮された電流の流れにくさを表しています。
コイルやコンデンサによる電流の流れにくさのことはリアクタンス[reactance]と呼びます。
リアクタンスの量記号はX、単位は[Ω]です。
従って、抵抗RとリアクタンスXとインピーダンスZの間には、以下のような関係が成り立っています。
Z=R+jX
周波数によって抵抗値が変化するものと変化しないものを分けてあるだけですね。
複素数表示になり、jは虚数を表しています。
3.アドミタンスとは?
アドミタンス[admittance]とは、インピーダンスの逆数のことです。
つまり、アドミタンスは交流回路における電流の流れやすさを表しています。
量記号はY、単位は[S]です。
インピーダンスの量記号はZなので、Z=1/Yになるということですね。
アドミタンスもインピーダンス同様に複素数表示され、実数部をコンダクタンス[conductance]、虚数部をサセプタンス[susceptance]と呼びます。
コンダクタンスの量記号はG、サセプタンスの量記号はBで、どちらも単位は[S]です。
従って、コンダクタンスGとサセプタンスBとアドミタンスYの間には、以下のような関係が成り立っています。
Y=G+jB
4.インピーダンスとアドミタンスの関係
インピーダンスとアドミタンスの関係をまとめると、以下のようになります。
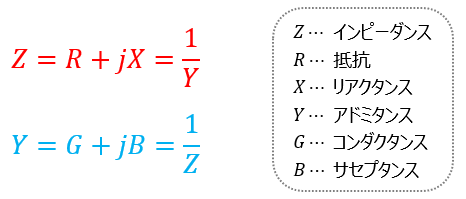
コンダクタンスは、直流回路において抵抗の逆数になります。
直流回路における電流の流れやすさを表しているんですね。
そのことから、リアクタンスの逆数もサセプタンスだと思った方はいませんでしょうか?
それ、間違いなので今のうちに正しておきましょう。
以下のようにはならないのです。
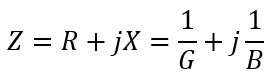
コンダクタンスは確かに抵抗の逆数ではあるのですが、“直流回路において”と付いていますよね?
要するに、交流回路においては逆数にならないんですよ。
リアクタンスという概念も関係してくるので、単純な逆数では無くなるんです。
だから、アドミタンスの実数部をコンダクタンス、虚数部をサセプタンスという難しい言い回しにしたんです。
実際に計算してみれば明らかなので、当て嵌めて整理してみましょう。
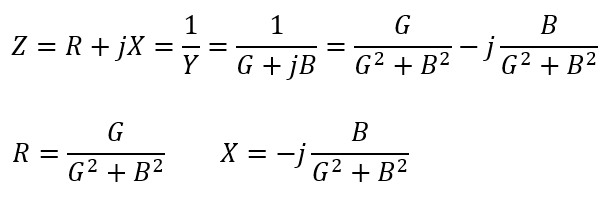
全然違うでしょう?
「インピーダンスとアドミタンスが逆数になっている。」
この点に注視しましょうね。
以上、「インピーダンスとアドミタンス」についての説明でした。




