今回は、「インダクタにかかる電圧と流れる電流の時間的変化」についての説明です。
1.ポイント
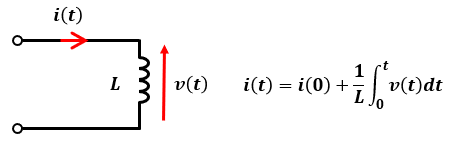
2.インダクタにかかる電圧と流れる電流の時間的変化
インダクタに電圧がかかるとインダクタに流れる電流が変化します。
ただ、当然即変化するわけがないです。
時間経過と共に変化します。
図1のようにインダクタにv(t)という電圧がかかっていた場合、電流の時間的変化i(t)は以下のように表せます。
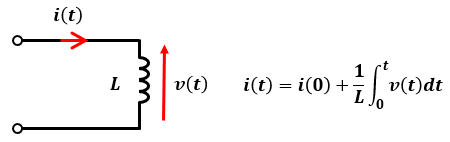
式だけ見てもよくわからないと思いますので、例を見ながら考えていきましょう。
L=10[mH]で、v(t)は0~2[ms]の間は10[mV]、2~4[ms]の間は-10[mV]になっていたとします。
この時のi(t)の時間的変化を図示してみましょう。
まず、0~2[ms]の間について考えます。
0[ms]時点では何も電圧がかかっていなかったので、当然ながら電流は流れていません。
その為、i(0)=0[mA]です。
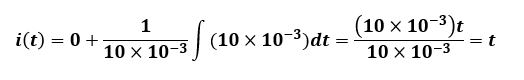
計算すると、0~2[ms]の間はi(t)=tになるようです。
これが0~2[ms]間のインダクタに流れる電流です。
つまり、1[ms]時点では1[mA]、2[ms]時点では2[mA]と変化するわけです。
次は2~4[ms]の間について考えます。
2[ms]時点では2[mA]の電流が流れていることがわかっているので、ここで言うi(0)は2[mA]になります。
後の考え方は先程と同じです。
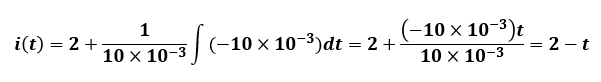
計算すると、2~4[ms]の間はi(t)=2-tになるようです。
これが2~4[ms]間のインダクタに流れる電流です。
ただ、この関係式はあくまでt=2[ms]時点を始点とした場合の関係式です。
なので、t=3[ms]時点では1[ms]経過、t=4[ms]時点では2[ms]経過と捉える必要があります。
つまり、3[ms]時点では1[mA]、4[ms]時点では0[mA]と変化するわけです。
もしくは、本当の意味でのi(0)を式に反映してください。
上記の説明ではi(2)をi(0)と置いています。
なので、そう置かなかった場合のi(t)は、i(t)=i(0)-tになります。
2[ms]時点では2[mA]の電流が流れているので、i(2)=2[mA]です。
つまり、i(2)=i(0)-2、2=i(0)-2、i(0)=4[mA]になります。
よって、i(t)=4-tとなります。
この状態ならt=3[ms]時点では3[ms]経過、t=4[ms]時点では4[ms]経過とそのまま捉えることができます。
自分なりにわかりやすい方法で計算しましょう。
以上の関係考慮してi(t)の時間的変化を図示すると、以下のようになります。
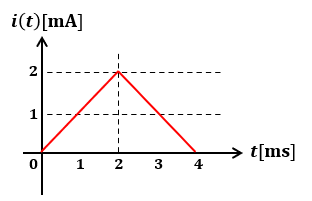
以上、「インダクタにかかる電圧と流れる電流の時間的変化」についての説明でした。




