今回は、「フレミング右手の法則」についての説明です。
1.ポイント
磁界中で導体を移動させた時、磁束(磁界)の方向と導体の移動方向に対応した向きへ電磁誘導により起電力が発生する。
この起電力の発生する方向を知るための方法。
2.フレミング右手の法則とは?
図1のように、磁界中に導体があります。
この導体を磁界中で移動させた時、磁束(磁界)の方向と導体の移動方向に対応した向きへ電磁誘導により起電力が発生します。
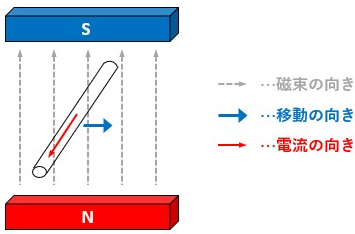
ここで起電力の発生する向きを知るための方法として、フレミング右手の法則があります。
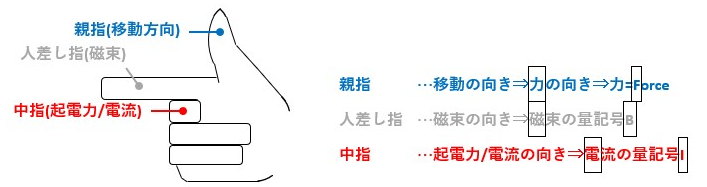
図2のように、右手の親指、人差し指、中指が互いに直角になるようにして中指が正面を向くような形にして下さい。(xyz軸を示すイメージ)
絵が適当なのは許して下さい、なんでもしますから。
この時、親指を導体の移動方向、人差し指を磁束の方向に合わせると、中指が起電力の発生する方向を示します。
覚え方は2パターンあります。
好きな方で覚えましょう。
- 親指、人差し指、中指の順に力(Force)、磁束(密度)(量記号B)、電流(量記号I)の向きを指し示しているので、FBIと覚える。
- 中指、人差し指、親指の順に電流、磁束、力の向きを指し示しているので、電磁力と覚える。
「フレミング左手の法則」と混同しないように注意しましょう。
こじ付けですけど、私は右手(migite)のmは動かす(move)のmだと覚えています(笑)
3.磁界と垂直方向に導体が移動する場合の起電力
磁界中で移動する導体にはフレミング右手の法則に従って起電力が発生するわけですが、その起電力の大きさについて考えていきます。
まずは、磁界と垂直方向(磁界を横切る方向)に導体が移動する場合についてです。
電磁誘導に関するファラデーの法則より、電磁誘導により発生する起電力の大きさe[V]は次のように表せます。
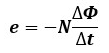
N[回]は巻数、Δt[s]は磁束変化時の経過時間、ΔΦ[Wb]は磁束の変化量を表しています。
以降は大きさについて考えていく為、符号は考えないものとします。
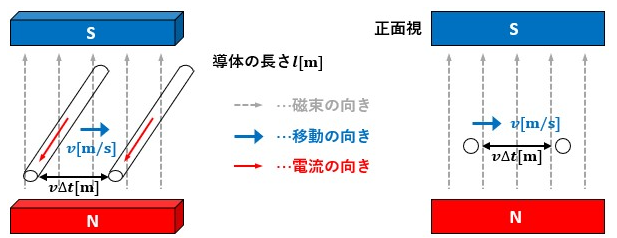
磁束密度B[T]の平等磁界中で有効な長さl[m]の導体が速度v[m/s]でΔt[s]間移動したとします。
この時、導体はv[m/s]×Δt[s]=vΔt[m]だけ移動します。
導体が移動した距離vΔt[m]に導体の有効長さl[m]を掛けると、磁界中を横切った面積ΔS[m2]が算出できます。
ΔS=vlΔt
磁束の変化量ΔΦ[Wb]は磁束密度B[T]に磁界中を横切った面積ΔS[m2]を掛けた値になるので、Δt[s]間当たりの磁束の変化量ΔΦ[Wb]は次のように表せます。
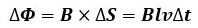
なので、導体に発生する起電力の大きさe[V]は以下のようになります。
※ 導体が移動することを念頭に置いている為、巻数N=1としています。
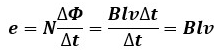
4.磁界と水平方向に導体が移動する場合の起電力
次に、磁界と水平方向(磁界と並行)に導体が移動する場合について考えます。
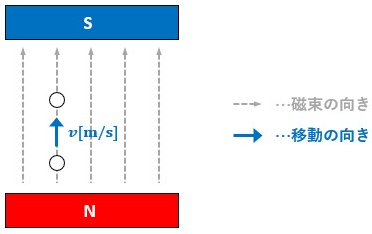
図4を見てわかる通り、磁界と水平方向(磁界と並行)に導体が移動するということは、磁束と同じ向きに移動するということです。
その為、時間がいくら経過したところで磁束は変化しません。
つまり、起電力は発生しません。
5.磁界を斜めに導体が移動する場合の起電力
ここまでの話で、磁界に対して垂直方向に導体が移動すると起電力が発生し、水平方向に導体が移動すると起電力が発生しないことがわかりました。
なので、垂直でも水平でもない斜め方向に移動した場合についても考えます。
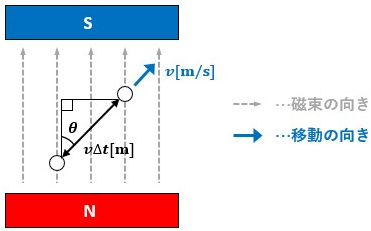
図5のように磁束に対して角度θの方向へ導体が移動したとします。
条件は磁界と垂直に移動した時同様に磁束密度B[T]の平等磁界中で有効な長さl[m]の導体が速度v[m/s]でΔt[s]間移動したとします。
この時、磁束の変化量ΔΦ[Wb]は磁束密度B[T]に磁界中を横切った面積ΔS[m2]を掛けた値になることに変わりはありません。
その為、結局考えるのは磁界と垂直に移動した方向に関してのみとなります。
垂直方向への導体の移動距離はvΔtsinθ[m]なので、導体に発生する起電力の大きさe[V]は以下のようになります。
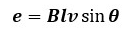
以上、「フレミング右手の法則」についての説明でした。




