今回は、「並列接続の考え方」についての説明です。
1.ポイント
2個以上の抵抗の両端を同じところに繋ぐ接続方法。
電圧が一定。
並列接続時の合成抵抗は、各抵抗値の逆数の和を求め、その値をさらに逆数にした値に等しい。
2個の抵抗を並列接続している場合、合成抵抗は和分の積になる。
電流が抵抗値の比で逆比例配分される。
レジが並列接続の良い例になるかと思います。
レジって一つしかないとそこに行列ができるので、基本的に複数個存在しますよね?
なので、お客さんが複数来たとしても、複数のレジに案内することでスムーズに対処が可能なわけです。
電気について学び始めだと、並列接続時の電圧と電流の関係で若干混乱する方がいるかもしれませんが、そんな時はこのレジをイメージしてみてください。
仕事が早い人がいるレジとモタモタしている人がいるレジだと、必然的に前者のレジに客が流れるでしょう?
ここでレジを抵抗、客を電子だと考えると、客(電子)が通りやすいレジ(抵抗値が低い抵抗)の方が人の流れ(電子の流れ=電流)が激しくなります。
これだけの話なんです。
2.並列接続
電気回路の接続方法には、「直列接続」と「並列接続」の2つの方法があります。
今回は、「並列接続」についての説明をしていきます。
2個以上の抵抗の両端を同じところに繋ぐ接続方法=並列接続ですので、以下のように複数の抵抗が繋がっている状態は並列接続されていると言えます。
ちなみに、R1は1個目の抵抗、Rnはn個目の抵抗を表しています。
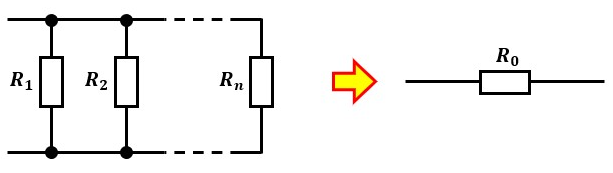
直列接続・並列接続に関わらず、抵抗成分は合成して1つの抵抗(合成抵抗と呼ぶ)にすることが可能です。
図1のR0が合成抵抗にあたります。
並列接続では、各抵抗値の逆数の和を求め、その値をさらに逆数にした値に等しくなります。
式で表すと、以下のようになります。
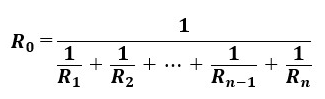
抵抗の逆数はコンダクタンスと呼ばれ、量記号はG、単位は[S]で表します。
この関係から、合成抵抗R0はコンダクタンスで表すことも可能です。
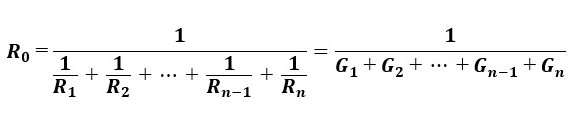
なぜ並列接続の合成抵抗が各抵抗値の逆数の和を求めてその値をさらに逆数にした値に等しくなるかと言うと、並列接続時は回路にかかる電圧が一定だからです。
R1とR2が並列接続されている回路(図2上)と、R1とR2の合成抵抗であるR0で構成される回路(図2下)を比較して考えてみましょう。
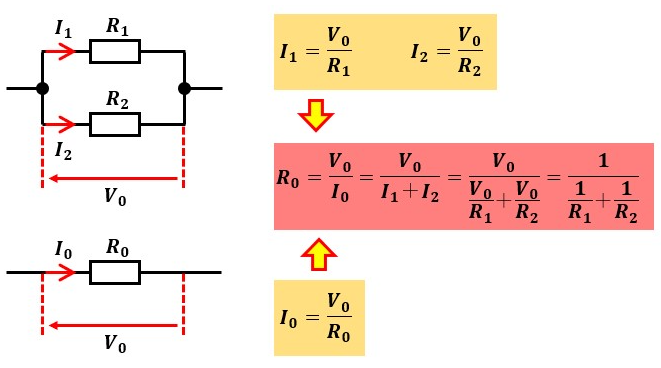
R1に流れる電流はI1、R2に流れる電流はI2、回路全体に流れる電流はI0です。
図2上と図2下のそれぞれの回路には同じ起電力の電源を繋いでいるので、回路全体にかかる電圧V0は同じになると考えてください。
オームの法則から、図2上と図2下の各抵抗に流れる電流を算出します。
計算した結果が橙塗り部分です。
I0=I1+I2の関係が成り立っているので、赤塗り部分が求められます。
この結果から、R0=1/(1/R1+1/R2)という関係が見出せますので、並列接続では各抵抗値の逆数の和を求めてその値をさらに逆数にした値が合成抵抗になると言えます。
また、2個の抵抗を並列接続した場合、合成抵抗は和分の積で求められます。
知っていると計算が容易になるので、覚えておきましょう。
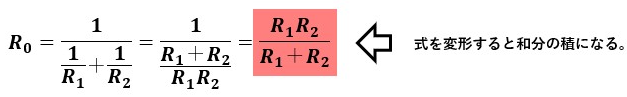
並列接続時に回路にかかる電圧が一定となる理由を簡単にまとめましたので、気になる方は以下のボタンを押して下さい。
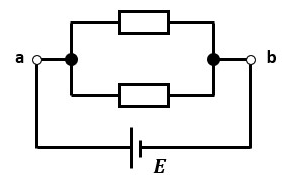
上図のように並列接続されている回路があるとします。
この回路の端子a-b間の電圧は、起電力がEなのでE[V]です。
a-b間で抵抗が何個並列に繫がっていても起電力は変化しない為、端子a-b間の電圧も変化することはありません。
また、並列接続時に回路にかかる電圧が一定である為、電流が抵抗値の比で逆比例配分されるという特性も出てきます。
図2にて、2つの抵抗が並列接続されている回路で、I1=V0/R1、I2=V0/R2という関係が成り立っていました。
この2式を変形すると以下のようになります。

つまり、回路全体の電流I0は、1/R1:1/R2の比で分けることができます。
これを逆比例配分と呼び、逆比例配分した各抵抗の電流(図2のI1、I2)のことを分路電流と呼びます。
図2の分路電流を式で表すと以下のようになります。

分路電流は、全体の電流(I0)に反対側の各抵抗値をかけて、合成抵抗で割ることで求められます。
つまり、I1を求めたいならR2、I2を求めたいならR1が分子にあたります。
また、3つ以上の抵抗を並列接続する場合も考え方は同じですが、若干注意が必要です。
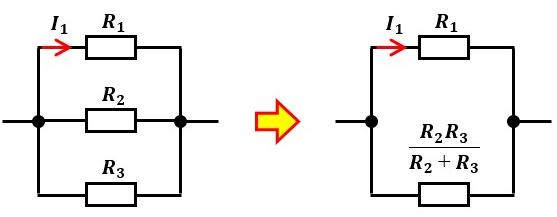
下図のように3個の抵抗が並列接続されている回路を例に考えます。
I1を逆比例配分で求めようとする場合、R2とR3の合成抵抗を計算して、2つの抵抗の並列回路にする必要があります。
ここでありがちなのが、R2とR3の合成抵抗を直列接続時のように各抵抗の和で求めてしまうというミスです。
間違えないようにしましょう。
以上、「並列接続の考え方」についての説明でした。



