今回は、「ド・モルガンの等価ゲートを用いた回路の簡単化」についての説明です。
1.ポイント
ド・モルガンの定理から考えられる等価回路。
ド・モルガンの等価NANDゲートとド・モルガンの等価NORゲートが存在する。
2.ド・モルガンの等価ゲートとは?
ド・モルガンの定理から、NANDゲートはORゲートとNOTゲート、NORゲートはANDゲートとNOTゲートを使って等価ゲートで表すことができます。
これらの等価ゲートのことを、ド・モルガンの等価ゲートと呼びます。
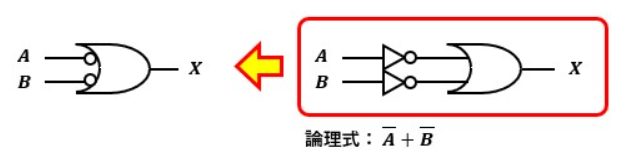
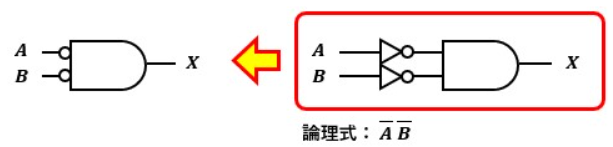
論理回路以外にも言えますが、回路構成は簡単にするに越したことはありません。
論理回路の場合、基本的な演算回路は以下のような種類がありました。
- AND回路
- OR回路
- NOT回路
- NAND回路
- NOR回路
- XOR回路
実際に回路を構成することを考えると、基本的な論理ゲートとはいえ別の種類の論理ゲートを多数組み合わせた時、この回路は簡単と言えるのでしょうか?
今回は、ド・モルガンの等価ゲートに置き換えることにより、使用ゲートの種類を減らして回路を簡単化する方法を説明していこうと思います。
3.ド・モルガンの等価ゲートを用いた回路の簡単化①
まずは簡単な例から見ていきましょう。
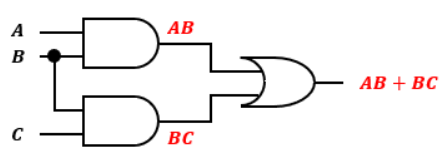
この回路をNANDゲートで構成してみます。
NOTゲートを2回通すと、入力が反転されたものが反転されて元に戻りますよね?
なので、図3のANDゲートとORゲートの間にNOTゲートを2つ繋いでも論理に変化はありません。
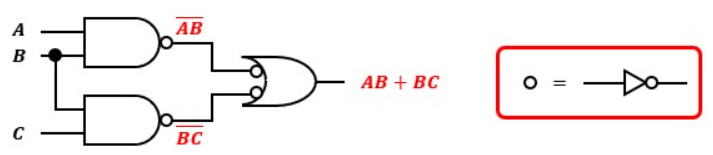
こうすると、右にあるORゲートがド・モルガンの等価NANDゲートになります。
ド・モルガンの等価NANDゲートはNANDゲートと置き換えが可能なので、図4は図5のように置換が可能です。
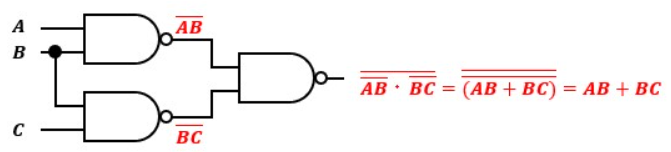
これでNANDゲートのみの回路構成になり、簡単化されました。
4.ド・モルガンの等価ゲートを用いた回路の簡単化②
次はもう少し複雑な例を見ていきましょう。
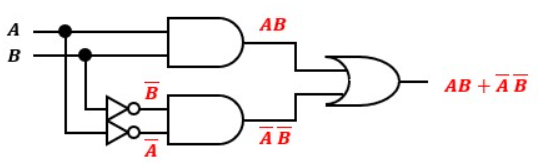
この回路もNANDゲートで構成してみます。
AND回路から右側は例①と全く同じ構成なので、図7のように置き換わります。
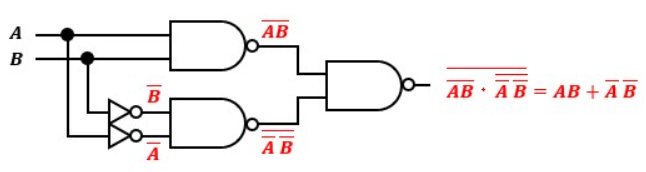
では、余っているNOTゲートはどうすれば良いでしょうか?
ここで、NANDゲートの入力が同じ場合について考えてみます。
NANDゲートは、2つの入力に対して1つの出力があり、入力が両方“1”の時に出力が“0”になる回路を指していました。
ここで言う2つの入力が1つの入力になるので、以下のようになります。

つまり、入力を同じ論理変数にしてしまえば、NANDゲートはNOTゲートとして使えるのです。
※ 同様の理由で、NORゲートもNOTゲートとして使用可能。
よって、NANDゲートのみの回路構成にすると以下のようになります。
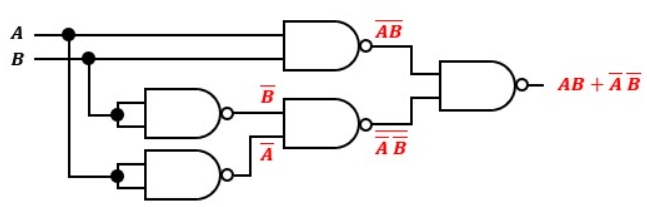
このように簡単化が可能です。
例はNANDゲートで表現するものしか挙げませんでしたが、NORゲートだけで構成することも可能なので、色々試してみましょう。
以上、「ド・モルガンの等価ゲートを用いた回路の簡単化」についての説明でした。




