【基礎から学ぶ論理回路】 ド・モルガンの等価ゲート

今回は、「ド・モルガンの等価ゲート」についての説明です。

１．ポイント

２．ド・モルガンの等価ゲートとは？

論理回路の重要な定理にド・モルガンの定理というものがあります。

ド・モルガンの定理は、以下の2式のことを指します。

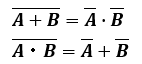
この関係から、NANDゲートはORゲートとNOTゲート、NORゲートはANDゲートとNOTゲートを使って等価ゲートで表すことができます。
これらの等価ゲートのことを、ド・モルガンの等価ゲートと呼びます。

３．ド・モルガンの等価NANDゲート

まずは、ド・モルガンの等価NANDゲートについて考えていきます。

通常のNANDゲートは以下の通りです。

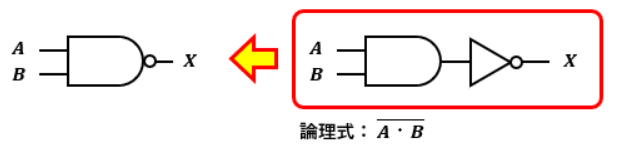
ド・モルガンの定理より、NANDゲートを通した場合の出力はAー+Bーと表すことが可能です。

つまり、NANDゲートはAーとBーを入力としたOR回路と言えます。

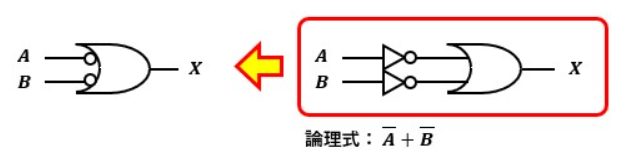
このように、入力側にNOTゲートを付けたORゲートのことをド・モルガンの等価NANDゲートと呼びます。

４．ド・モルガンの等価NORゲート

次は、ド・モルガンの等価NORゲートについて考えていきます。

通常のNORゲートは以下の通りです。

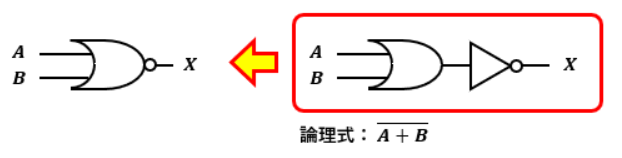
ド・モルガンの定理より、NORゲートを通した場合の出力はAー・Bーと表すことが可能です。

つまり、NORゲートはAーとBーを入力としたAND回路と言えます。

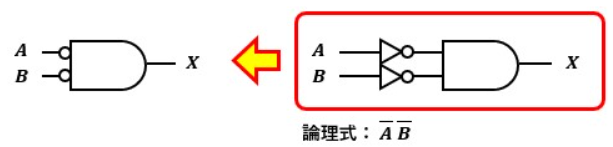
このように、入力側にNOTゲートを付けたANDゲートのことをド・モルガンの等価NORゲートと呼びます。

以上、「ド・モルガンの等価ゲート」についての説明でした。

---