今回は、「ド・モルガンの定理」についての説明です。
１．ポイント
ド・モルガンの定理
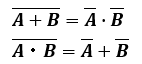
２．公理と定理
論理回路には公理と定理が存在します。
公理…理由なく正しいこと。
定理…公理から導き出された正しいこと。
つまり、前提知識・基礎知識みたいなヤツです。
公理と定理は結構な数があり、本当に基本的過ぎて特に覚えるように意識する必要の無いものも存在します。
この定理の中にド・モルガンの定理というものがあり、この定理は論理式の変形に頻繁に使用されます。
なので、本記事ではどんな定理なのか、どのように使用するのかを簡単に説明していこうと思います。
３．ド・モルガンの定理
ド・モルガンの定理は、以下の2式のことを指します。
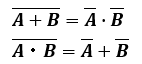
簡単に言えば、論理和と論理積で置き換えが可能な定理です。
論理和と論理積が何かわかっていない場合は、先に以下の記事を確認して下さい。
【基礎から学ぶ論理回路】 真偽と真理値表
電子回路を構成する部品の中には、信号を反転させたり、複数の入力信号の状態の組み合わせによって出力信号を変えるようなものが存在します。きちんと筋道を立てて考える思考のことを“論理的”と言いますので、このような回路のことは論理回路と呼びます。本記事では、そんな論理回路の種類や実際の構成について、わかりやすく解説していきます。今回は真偽と真理値表についてです。
www.elmusicwisdom.site
2023.01.27
４．ド・モルガンの定理の使用例
では、ド・モルガンの定理の使用例を載せていきます。
例題1
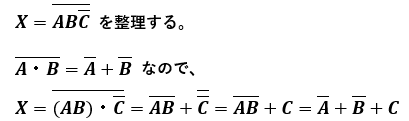
これでXは単純な論理和で形成されていることがわかりました。
例題2
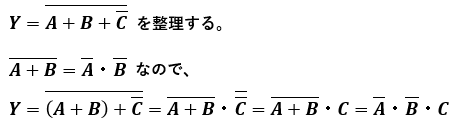
これでYは単純な論理積で形成されていることがわかりました。
このように、ド・モルガンの定理を使用することによって、一見複雑な論理式を単純な論理和や論理積で表すことが可能になります。
以上、「ド・モルガンの定理」についての説明でした。
