【基礎から学ぶコンデンサ】 電界と電位の関係 ～点電荷と平行板間の電位について～

今回は、「電界と電位の関係」についての説明です。

１．ポイント

２．電位とは？

電界中で+1[C]の単位正電荷に働く力の大きさが電界の強さでした。
これに対し、電界中で+1[C]の単位正電荷が持つ位置エネルギーが電位です。
電位は量記号V、単位は[V]もしくは[J/Cジュール毎クーロン]です。

上述の通り、電界中に単位正電荷が存在すると静電力が働くので、力の方向に単位正電荷が移動しようとします。
電界中に存在する単位正電荷がその場に静止するために、位置エネルギーである電位を持っているという認識です。

q₁[C]の電荷が媒質中に存在している場合について考えます。

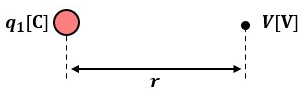
この電荷からr[m]だけ離れた点の電位V[V]を式で表すと以下のようになります。

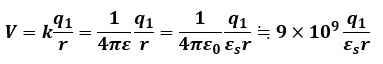
※ ここで言う電位Vとは、厳密には無限遠(静電力の働いていない場所)から単位正電荷を運ぶエネルギーを指しています。

電位は、ベクトル量(大きさ＋方向)ではなくスカラー量(大きさのみ)です。

例を用いて説明します。

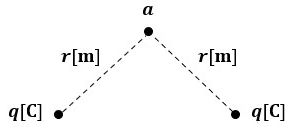
図2のように真空中(誘電率ε₀)に2つの電荷q[C]があります。
この2つの電荷から距離r[m]の位置である点aの電位を求めます。

片方の電荷による点aの電位は以下のようになります。

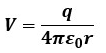
電位はスカラー量なので、点aの総電位V_a[V]は単純に各電荷による電位の和になります。

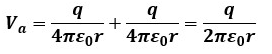
次に、2点間の電位差(電圧)について考えてみます。
電荷からr₁[m]離れた点の電位V₁[V]とr₂[m]離れた点の電位V₂[V]があります。

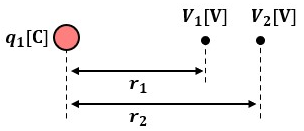
電位は距離に反比例している為、電荷に近い程電位が大きくなります。
つまり、V₁>V₂になっています。
その為、2点間の電位差V₁₂[V]は以下のようになります。

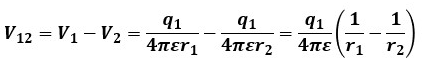
ここで言う電位差V₁₂[V]は、r₂[m]離れた点からr₁[m]離れた点まで移動するためのエネルギーになります。

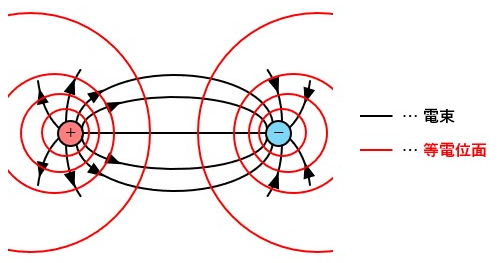
３．等電位面

電位の等しい箇所を繋いだ時にできる面を等電位面と呼びます。

等電位面は以下のような性質を持っています。

４．平行導体板間の電界と電位の関係

図5のように導体板が平行に2枚並んでいて、導体板に電源が繋いであります。

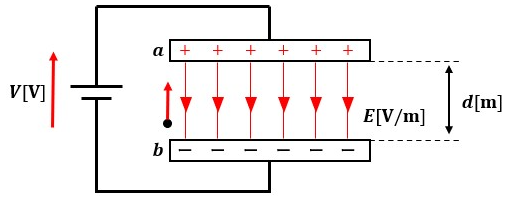
平行導体板間の電界の強さをE[V/m]、導体板間の電位差をV[V]、導体板距離をd[m]とした時、+1[C]の単位正電荷を電界から受ける力に逆らって移動させる(bからaの方向)のに要する仕事はV[V]です。

単位正電荷に働く力の大きさは電界の強さに等しい為、aからbの向きにはE[N]の静電力が発生しています。
力×距離=仕事なので、単位正電荷が静電力E[N]で距離d[m]だけ移動した時の仕事はE×dになります。
つまり、単位正電荷をaからbまで移動させるのに必要な仕事がEdなので、逆にbからaまで移動させるのに必要な仕事もEdと言える為、Ed=Vが成り立ちます。
よって、電界の強さは単位である[V/m]からもわかる通り、以下のように表せます。

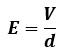
以上、「電界と電位の関係」についての説明でした。

---