今回は、「dBAという単位と人間にとっての音の聴こえ方について」についての説明です。
1.初めに
dB(デシベル)とは、電力や音の強さの比較・減衰などを表す時に使用する単位のことです。
詳しくは過去の記事にまとめてあります。
さて、このdBですが、表現方法の違いとしてdBm/dBμ/dmu/dBv/dBVのような種類があります。
これらの単位は、1mVを0dBmと定義した時の電圧の単位(dBm)だったり、0dBを0.775Vと定義した時の電圧の単位(dBu)だったりと、dB表示をする対象とその基準を定めて運用しています。
これらの単位についても既にまとめてあります。
今回は、これらの単位とはまた別のdBAという単位にフォーカスして解説していこうと思います。
2.dBAとは?
dBAとは、dB同様に音の強さを表す単位です。
ただし、dBの場合は人間の可聴領域における音の聴こえ方を考慮した補正をしていませんが、dBAは人間の可聴領域における音の聴こえ方を考慮した補正をしています。
dBは音の強さを表す単位なので、人間の耳にとって高い音に聴こえようが低い音に聴こえようが、“音の強さ”という観点では同じ数値になることがあります。
なので、機械によって数値化した際に同等のdBになる音があったとしても、それらの音は人間にとっては同等に感じられない可能性があります。
その為、音響・オーディオ機器の騒音レベルを表す単位の単位なんかは、人間の耳に配慮したdBAが用いられていることがあります。
オーディオ機器の音はあくまで人間が聴くものなので、人間基準で考えないと意味が無いですからね。
室内を想定している場合の騒音レベルはNC値というもので表していたりもしますが、この辺の説明はまた別途まとめます。
今説明するとややこしくなりますのでね…。
3.音圧レベルの算出方法
dBAが実際にどのように表現されるのかを説明するには、音圧(音が大気を押す力)のレベルの表し方についても理解しておく必要があります。
本来、音圧は大気圧の変動なので単位をPa(パスカル)で表していたのですが、Paのまま表現すると数値の上下が非常に大きくなって使いづらいというデメリットがありました。
そんな時に役立つのがdB表記です。
dBなら指数関数的に値が変化したとしても表現できますからね。
具体的には、人間の最小可聴音圧は1kHz/20μPaだと言われていた為、20μPaを基準音圧とした時の相対量の比率を音圧レベル(dB表記)と定義するようになりました。
計算式で表すと以下の通りです。
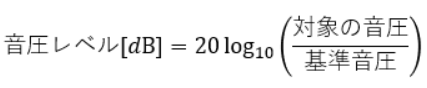
基準音圧が20μPaなので、この基準に対してどの程度の比率になっているのかを表現していますね。
この式を見てわかる通り対数表現をしていますので、20dB上がる毎に音圧は10倍になります。
0dBでは音圧20μPa、20dBでは音圧200μPa、40dBでは2,000μPa…20dB上がると音圧が10倍になっているでしょう?
そもそも対数をよくわかってない場合は、以下の記事を参考にしてください。


4.人間にとっての音の聞こえ方
先程述べたように、人間の耳では同じ音圧の音だとしても、高い音に聞こえたり低い音に聞こえたりします。
音は空気の振動で、その振動の周波数に合わせて耳の各器官も振動することで、人間は“音”というものを認識しています。
そんな原理をしているので、周波数が高いと高い音に聞こえ、周波数が低いと低い音に聞こえます。
この高い低いという感覚なのですが、人間の感覚で聞き分けるのにも限度があります。
それがいわゆる可聴領域です。
聴力検査で、高い音は聞き取りづらかったりするでしょう?
アレは、音が小さいから聞こえないのではなく、周波数が高いから聞こえないのです。
低い音に関しても同様です。
その為、可聴領域における中音域に値する周波数帯の音は良く聞こえるのですが、可聴領域ギリギリの周波数に近づくにつれて基本的に音が聞こえづらくなります。
具体的な数値で言うと、人間の可聴領域が20Hz~20KHzくらいで、2kHz~4kHz程度の音が特に聞こえやすく、20Hzと20kHzに近づくほど音が聞こえづらくなります。
この特性をグラフで表したものを等ラウドネス曲線と呼びます。
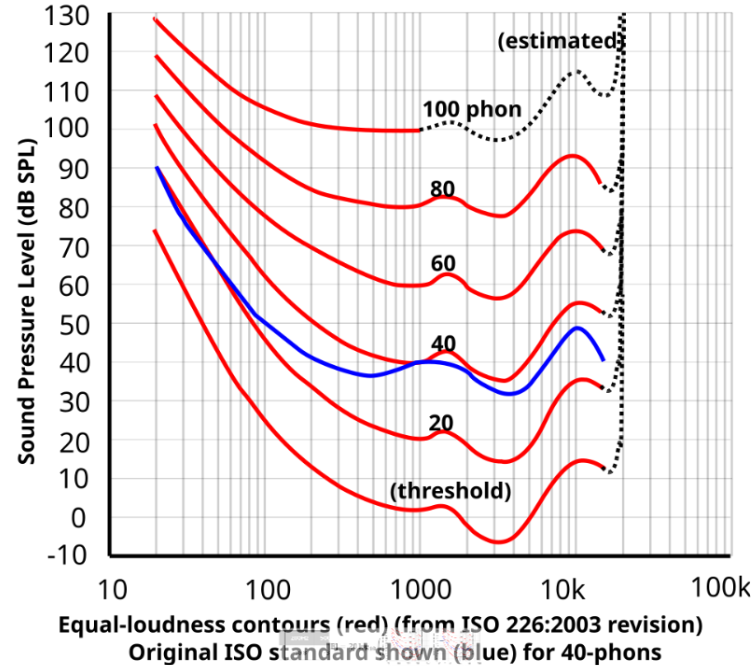
等ラウドネス曲線とは?
ラウドネス[Loudness]とは、人間が耳で感じ取る音の大きさのことです。
等ラウドネス曲線は、音量を一定として周波数を上げ下げした際に、人間にとって音量が一定に聞こえるように音圧レベルを調整した点を結ぶことで作成されています。
図1における赤線のことです。
phonというのは、ラウドネスレベルの単位です。
フォンもしくはホンと読み、dBと関連付けた単位になります。
等ラウドネス曲線は音量を一定として周波数を上げ下げして求めたものだと述べましたが、この時に基準にしているのが1kHzです。
なので、1kHz地点では、20phonが20dB、40phonが40dBという具合に、音圧レベルの値がそのままphonになるように定義されています。
要するに、同じphon値の音が各周波数においてどの程度聞こえやすいのかを一つの曲線で表していて、そもそものphon値が異なる(元々の音量が大きい/小さい)複数の条件における変遷を一つのグラフに収めて描写してあるだけです。
等ラウドネス曲線の見方についても一応解説しておきますね。
例えば、1kHzの音を20phonの音で聞きたいのなら20dBにする必要があります。
これに対して、40Hzの音を20phonで聞きたいのなら70dBにする必要があります。
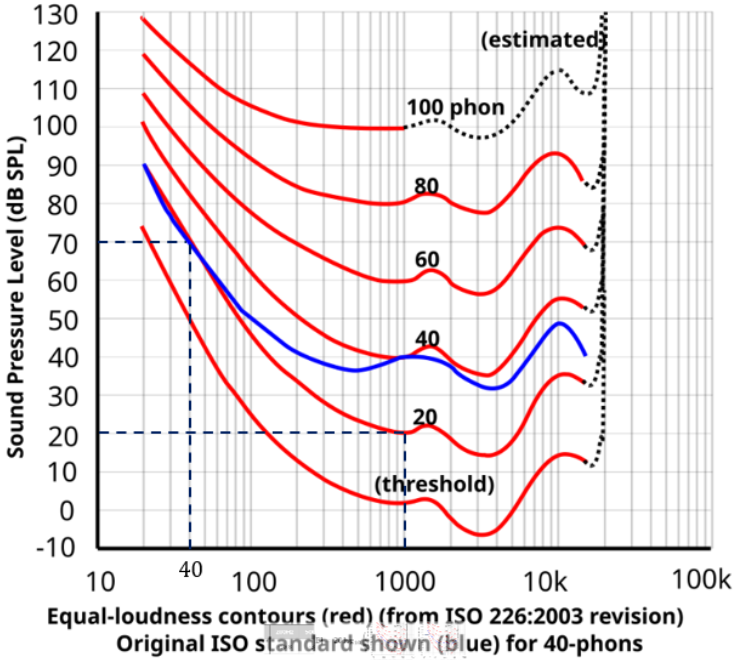
音圧レベルは20dB上がる毎に音圧が10倍になると述べましたよね?
つまり、20phonにおいては、1kHzの音の方が40Hzの音よりも100倍以上聞こえるようになっているのです。
その為、複数の楽器にて演奏をした場合、周波数の違いでよく音が聴こえる楽器とよく音が聴こえない楽器が出てくることになります。
その辺りの違いも考えて音量の調整が必要なんです。
まあ、同じ音圧レベルに揃えたら音同士で潰し合うので、想像以上にバランスを取るのは難しいんでしょうけどね。
等ラウドネス曲線は“人間にとって”音量が一定に聞こえるような音圧レベルを調べたものなので、当然ながら音量が一定になると判断しているのは人間になります。
その為、被験者複数人による統計データとなっていて、聞こえ方には個人差があります。
基本的には加齢による聴力の衰えがない若い年代の方を対象にデータを取得しているはずですので、高齢者の方は等ラウドネス曲線を下方修正してみた方が良いことになります。
あくまで参考値と考えておきましょう。
ちなみに、平仮名でホンと書いてしまうとまた別の単位になってややこしくなるので、必ずphonと記載する必要があります。
ホンは今は使われなくなった日本独自の単位なのですが、こちらも音に関する単位(騒音レベルの単位)なので考え始めると泥沼に嵌まり兼ねません。
必ずphonと記載してください。
図1の青い曲線はスルーしていましたが、一応補足説明しておきます。
この曲線は、1soneの時の周波数-音圧レベル曲線です。
soneとは、ラウドネスの単位でソーンと読みます。
周波数1kHzで音圧レベルが40dBの音を聞いたときの音の大きさを1soneと定義しています。
定義なのでそういうものとして覚えてもらう他ないです。
5.dBAの本質
ここまでの説明で、人間の耳では周波数によって音の聞こえ方が異なるという点は理解してくれたかと思います。
なので、普通に機械で取得したデータから音圧レベルをdBで表現しても、人間にとっては意味の無いものになります。
だから、人間の耳に合わせた補正が必要になります。
では、どのように補正すれば良いでしょうか?
答えは、「等ラウドネス曲線に合わせた補正をしてあげれば良い」です。
実際の計算式は見たところで理解できないので割愛しますが、等ラウドネス曲線に従って人間の耳の聴覚特性を考慮した補正を加えた音圧レベルのことをA特性音圧レベルと呼びます。
このA特性音圧レベルの単位がdBAなのです。
dBAの“A”は何のことなのかがこれでわかりました。
dBの“A特性”って言っているだけなんですよ、この単位は。
その為、dBAの読み方はただの「デシベル」となります。
“A”は読まなくて良いのです。
このA特性はJIS規格やIEC規格で規格化されているので、音響業界にて広く利用されています。
例えば、JIS規格(JIS Z 8731)には、以下のように記述されています。

この補正値を実際の音圧レベル(dB)に足し合わせたものが、人間にとっての音圧レベル(dBA)になります。
なので、音圧レベルの単位がdBAになっていたら、『人の耳で聞くことを考慮して補正してあるんだな』と思ってくれれば大丈夫です。
ちなみに、等ラウドネス曲線の特性を落とし込んだのがA特性とは言いましたが、あくまで近似式という点は念頭に置いといてください。
計算しやすいように単純化した式から導き出しているので已む無しです。
C特性とZ特性と騒音レベル
音圧レベルに対して人間の耳の聞こえ方を考慮した補正をするのがA特性でした。
基本的にA特性くらいしか耳にすることは無いのですが、音圧レベルを測定する際の補正の種類として他にもC特性とZ特性というものがあるので、一応解説しておきます。
C特性は、一律で平坦な重み付けをした補正です。
A特性は等ラウドネス曲線を考慮して周波数毎に補正値を変えていましたので、所々で重み付けの程度が変わっていました。
C特性の場合は、これが一定値になるのです。
つまり、人間にどう聞こえるのかは特に考慮しない補正ということになります。
それに何の意味があるのかと疑問に思うかもしれませんが、高周波数領域(8kHz以上)及び低周波数領域(31.5Hz以下)における測定をする際に影響を抑えることが可能になるらしいです。
昔は大きな音の測定ではこの評価方法が採用されることもあったようですが、現代ではあまり使われる機会が無くなっているようです。
Z特性とは、重み付けをしない純粋な音圧レベルのことです。
フラット特性と呼ばれていることもあります。
要するに、補正無しのただの音圧レベルです。
人間の耳など気にせずに、純粋にどの程度の音が発生しているのかという機械的な音圧データ欲しいのなら、Z特性での測定になります。
電車・飛行機のような人工物や川・滝のような自然物といったものの環境音をそのまま測定する際などに用いられます。
なので、C特性よりは使用される機会は多いです。
簡単にまとめますね。
まず、音圧レベルの測定をする際の補正には、A特性・C特性・Z特性の3種類が存在します。
人間の聴覚を考慮した音圧レベルを測定したいならA特性を用いますので、音響関連の業務や人間の活動領域が近い場所の騒音を測定する場合は、大概A特性を用いることになります。
環境音のような生の音圧データを測定したいのなら補正をする必要が無いので、Z特性を用います。
C特性は大きな音の測定に昔は使われていましたが、最近はあまり使われなくなっています。
こんな感じです。
ちなみに、音圧レベルに対してA特性の補正を加えたもののことを騒音レベルと呼びます。
人間の感じ取り方を加味して補正した音圧レベルを指しているので、人間が騒音だと感じるレベルの指標になりますからね。
dBAなのにdB表示していることがある
基本的には人間の聴覚特性を考慮した補正をしているのなら単位がdBAになっているはずなのですが、例外もあります。
それは、環境基準における騒音レベルの単位です。
理由は単純で、環境基準における騒音レベルはA特性音圧レベルしか取り扱わないからです。
元々、dBAはA特性補正をしているという目印として“A”を付けていました。
なので、『dBと混同する可能性が無いのなら“A”は取っ払ってしまえ!』というわけです。
ただ、単位をdBにする場合は、A特性を表すために「LA ○○dB」という具合に先頭に“LA”を付けて表記する必要があります。
なので、表記上A特性補正をしているかどうかは最低限見分けが付くようにルール付けはされています。
結局はdBAならdBAだとわかるようにはしてあるのです。
なので、騒音レベルなのにdBとだけ表記するのは止めましょうね。
ちなみに、公的な規格では、寧ろこちらの表示形式の方が推奨されています。
私は日常的にはdBAしか見たことが無いですけどね。
みんな「ディービーエー」って言ってますよ。
また、C特性なら“LC”、Z特性なら“LZ”と表記されるようになります。
LAの場合は[A-Weighted Sound Pressure Level]の略称になるようなので、LevelAという表示なのかもしれませんね。
以上、「dBAという単位と人間にとっての音の聴こえ方について」についての説明でした。




