今回は、「ビオ・サバールの法則」についての説明です。
1.ビオ・サバールの法則とは?
ビオ・サバールの法則とは、導体に電流が流れた際にある点Pに作られる磁界の大きさを定義している公式のことです。
「磁界と電流の関係」の説明で直線導体と円形導体に電流が流れた際の磁界の強さを表した式が出てきましたが、これらの関係式はビオ・サバールの法則に基づいて導き出されています。
つまり、本記事はその補足説明が主になっています。
図1のように導体に電流Iが流れていたとします。
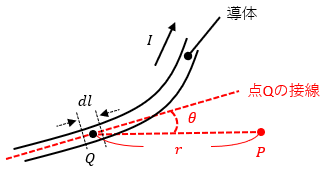
この時、導体上のある点Qが点Pに対して作る磁界の大きさは、以下のように定義されています。
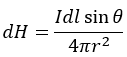
これが、ビオ・サバールの法則です。
dlは点Qの微小な導体の長さ、θは点Qの接線と点Qから見た点P方向の線のなす角を表しています。
あくまで微小な導体が作る磁界の大きさを表しているのでdHになっています。
なので、導体に流れている電流全体が作る磁界の大きさを求めたい場合は、導体上の無数にある点が作る磁界を足し合わせて求める必要があります。
つまり、積分しろということですね。
そうして積分した結果、直線導体や円形導体がある点に作り出す磁界の強さの関係式が導き出せるわけです。
例として、直線導体(無限長)と円形導体の磁界の関係式を実際に計算して導き出してみようと思います。
2.直線導体(無限長)の磁界の大きさ
アンペアの周回路の法則にて、直線導体(無限長)に電流I[A]が流れていて、導体の中心からx[m]離れた位置に発生する磁界の強さH[A/m]はH=I/2πxだとされています。
まずは、ビオ・サバールの法則からこの式を導き出してみます。
直線導体に流れる電流をI、直線導体上の任意の点Qの微小導体をdl、点Qの接線と点Qから見た点P方向の線のなす角をθ、点P-点Q間の線分の長さをrとします。
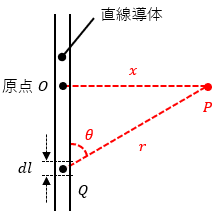
この時の点Pに対して作る磁界の大きさを考えると、ビオ・サバールの法則がそのまま当て嵌まることがわかります。
この導体が無限長になるので、積分の範囲が+∞~-∞ということになります。
まずは式を整理していきます。
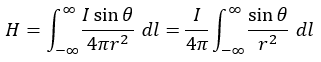
定数をインテグラル(積分記号のこと)の外に出しましたが、変数であるθとrが残ってしまいました。
このままではdlについて積分ができませんので、変数と微分記号を合わせる必要があります。
そこで、点Pから導体に向けて伸ばした垂線である距離xを利用していきます。
ここの距離は変化しない定数ですからね。
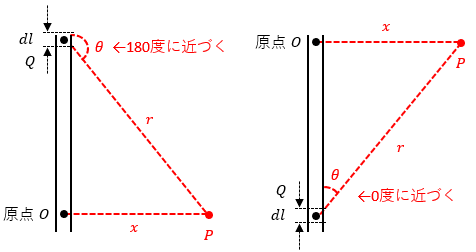
点Pから導体に向けて伸ばした垂線の交差点を原点Oとしてxとlを求めると、x=rsinθ、l=-rcosθになります。
※ 原点Oから上側が+∞方向、下側が-∞方向としているので、lの符号はマイナスになります。
この2式からrを取り除くと、l=-xcosθ/sinθになります。
この式をθで微分すると、以下のようになります。
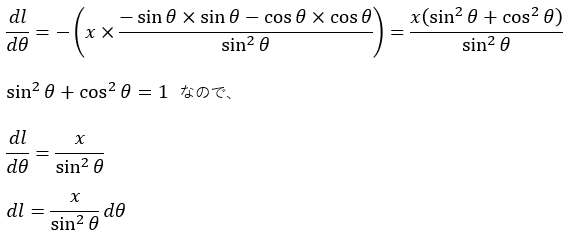
これでdlをdθに変換できるのですが、lに関する式からθに関する式に変化するので、積分範囲も変化します。
原点Oからlを+∞に引き延ばすとθはπに近づき、原点Oからlを-∞に引き延ばすとθは0に近づきます。
よって、θに関する式に変換すると、以下のようになります。
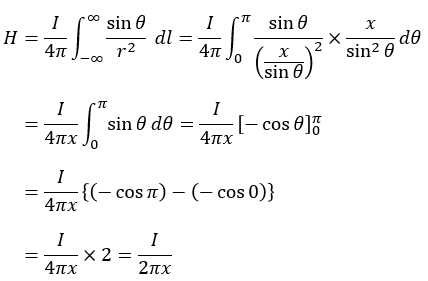
こうして直線導体(無限長)の磁界の大きさの公式が導き出されます。
3.円形導体の磁界の大きさ
半径x[m]の円形導体に電流I[A]が流れている時、円形導体の中心に発生する磁界の強さH[A/m]はH=I/2xになるとされています。
今度はこの関係式を導き出してみましょう。
円形導体に流れる電流をI、円形導体の中心を点O、円形導体の中心軸上の任意の点を点P、円形導体上の任意の点Qの微小導体をdl、点Qの接線と点Qから見た点P方向の線のなす角をθ、点P-点Q間の線分の長さをrとします。
この時の点Pに対して作る磁界の大きさから考えていきます。
ビオ・サバールの法則の定義式とほぼ同じになるのですが、一点のみ異なります。
それは、点Qの接線と点Qから見た点P方向の線のなす角θです。
直線導体の時はこのθが変化するのでビオ・サバールの法則をそのまま適用していたのですが、円形導体の場合はθが常にπ/2(直角)になります。
つまり、sin(π/2)=1なので、dH=Idl/4πr2となります。
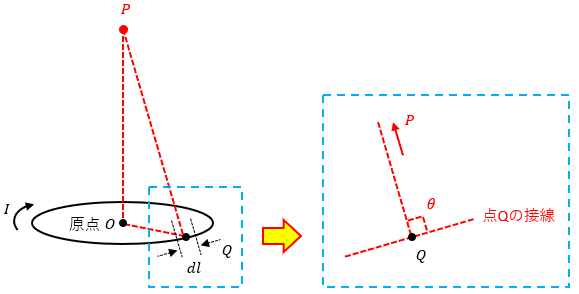
ここで点Pに作られる磁界について考えてみます。
線分O-Pを軸に左右対称になる点Aと点Bが点Pに作る磁界について図示すると、図5のようになります。
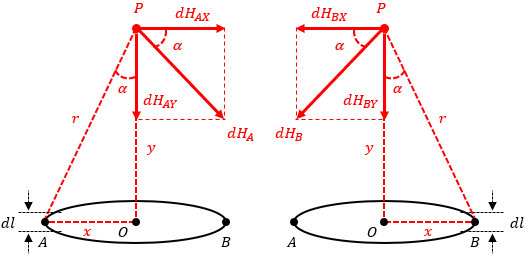
円形導体に流れる電流は一定なので、円形導体上のどの点が作る磁界でも、磁界の大きさ自体は同等です。
ということは、水平方向の磁界であるdHAXとdHBXは大きさが同じでベクトルが対称になっているので、互いに打ち消し合います。
導体の形状は円形になっているので、この現象は他の点でも発生します。
つまり、水平方向の磁界の大きさは0になって、垂直方向の磁界しか残らないんですね。
その為、円形導体の場合はdHではなくdHYについて考える必要があります。
図5に示したように∠APOをαと置くと、dHY=dHsinαと表せます。
この式にdHを代入すると、dHY=Idlsinα/4πr2になります。
このdHYを円周分(2πx)足し合わせることでHYが求まります。
よって、HYは以下のようになります。
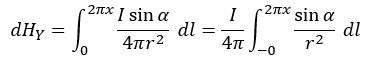
直線導体の時と同様にこの形ではdlについて積分ができませんので、一工夫が必要です。
∠APOの角度はαなので、三平方の定理を使ってsinαとrを定数であるxとyに置き換えます。
r=√(x2+y2)
sinα=x/r=x/√(x2+y2)
この2式を代入すると、以下のようになります。
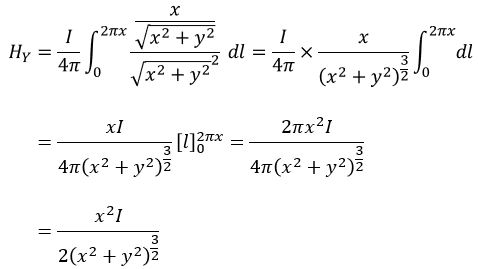
これで円形導体の中心軸上の任意の点である点Pの磁界の大きさがわかりました。
では、円形導体の中心の磁界の大きさはどうなるでしょうか?
単純な話、y=0を代入するだけですよね?
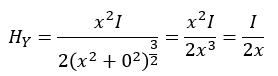
こうして円形導体の中心に発生する磁界の大きさの公式が導き出されます。
4.半円導体の磁界の大きさ
ついでなので半円導体の磁界についても考えてみます。
電検三種の理論分野の過去問にも出てきたことがあるので、知っておいて損することはないですよ?
各条件は円形導体と同じとします。
半円になると何が変わるかと言うと、水平方向の磁界が打ち消し合うという点が変わります。
半周しかしてくれないから、打ち消し合ってくれないんですよ。
ということは、任意の点Qが点Pに対して作る磁界の大きさは、dH=Idl/4πr2のままが正しくなります。
水平方向とか垂直方向とか考える必要がないのです。
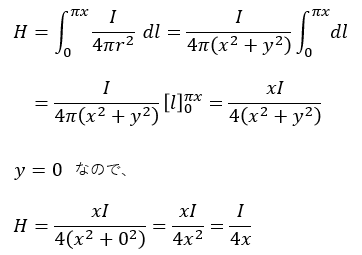
ということで、半円導体の中心に発生する磁界の大きさはI/4xと円形導体のちょうど半分になることがわかります。
これを書いていて思ったのですが、円形導体の時に垂直方向と水平方向に分けて考えた意味はあったのでしょうかね?
調べると出てくる解法を自分なりに解釈してまとめたわけですが、最初からdH=Idl/4πr2の式で計算しても答えが出るような気がするんですよね…。
この辺りがはっきりしたら内容を更新するかもしれません。
以上、「ビオ・サバールの法則」についての説明でした。




