今回は、「交流回路のオームの法則」についての説明です。
1.交流回路のオームの法則
交流回路についてですが、直流回路同様にオームの法則が適用可能です。
ただ、直流回路では負荷は抵抗Rのみでしたが、交流回路では誘導性リアクタンスXL、容量性リアクタンスXCという2つの要素についても考慮する必要が出てきます。
リアクタンスとは、コイルやコンデンサといった周波数によって抵抗値が変化する素子の電流の流れにくさのことを指しています。
コイルには電磁誘導などの作用があるので誘導性、コンデンサには静電容量というコンデンサに電荷を蓄える能力を表した定数があるので容量性と呼んでいる…のかもしれませんね
実際のところは不明ですが、覚える分にはこのイメージで良いでしょう。
誘導性リアクタンス
コイルの電流の流れにくさのこと。
量記号はXL、単位は[Ω]。
リアクタンスの量記号はXなので、そこにコイルの性質を表す定数であるインダクタンスLがくっついた量記号になっています。
誘導性リアクタンスXLの値は角速度ω[rad/s]、周波数f[Hz]に比例する。
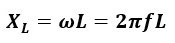
Lはインダクタンスと言い、コイルの性質を表す定数です。
単位は[H]。
詳しくは以下の記事にて触れていきますので、ここでの説明は割愛します。
コイルは、直流電流は妨げないが、交流電流を妨げる作用がある。
図記号はコイルを見立てた円弧が4つ繋がった形状を表している。
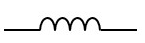
容量性リアクタンス
コンデンサの電流の流れにくさのこと。
量記号はXC、単位は[Ω]。
リアクタンスの量記号はXなので、そこにコンデンサの静電容量Cがくっついた量記号になっています。
容量性リアクタンスXCの値は角速度ω[rad/s]、周波数f[Hz]に反比例する。
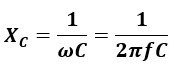
Cは静電容量と言い、コンデンサに電荷を蓄える能力のことです。
単位は[F]。
詳しくは以下の記事にて触れていきますので、ここでの説明は割愛します。
コンデンサは、交流電流は流すが、直流電流は流さない。
(厳密には交流電流が流れているように見えるですが今は気にしなくてOK)
図記号はコンデンサを見立てた金属板が2枚並んだ形状を表している。
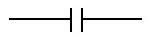
また、抵抗R、誘導性リアクタンスXL、容量性リアクタンスXCの何れかを含む交流回路全体の電流の流れにくさのことをインピーダンスと呼びます。
量記号はZ、単位は[Ω]です。
回路構成によっては、Z=R、Z=R+XL、Z=R+XL+XCなど、色々なパターンが考えられます。
最初に述べた通り、交流回路でもオームの法則は適用される為、以下の関係が成り立ちます。
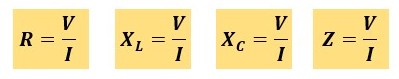
以上、「交流回路のオームの法則」についての説明でした。






