【基礎から学ぶコンデンサ】 2つの電荷が作る等電位面の求め方

“コンデンサ”という部品は、電気製品なら必須レベルで多用されています。
電気を蓄えたり放出したり、ノイズ成分を吸収したり、何かと便利だからです。
本記事では、そんなコンデンサという部品についての知識をわかりやすくまとめてみました。

今回は、「2つの電荷が作る等電位面の求め方」についての説明です。

「電界と電位の関係」の復習ですが、電荷q[C]からr[m]だけ離れた点の電位V[V]を式で表すと以下のようになります。

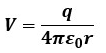
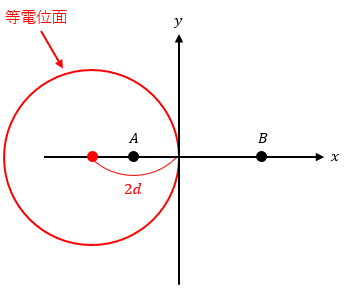
今、図1のように真空中に2つの点電荷が存在するとします。

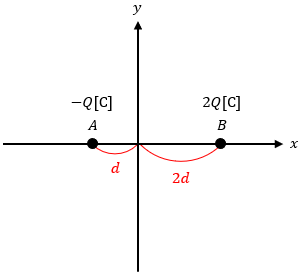
この時、電位が0[V]になる等電位面がどのような形を描くのか求めてみます。

電位が0[V]になるということは、点電荷A及び点電荷Bの電位がイコールになるということです。
なので、まずは点電荷Aの電位V_Aと点電荷Bの電位V_Bを求めます。

電位が0[V]になる座標をP(x,y)と置きます。
点Pと点A、点Pと点Bを一直線に結んだ斜線が公式の距離r[m]に該当するので、三平方の定理からそれぞれの距離を求めていきます。

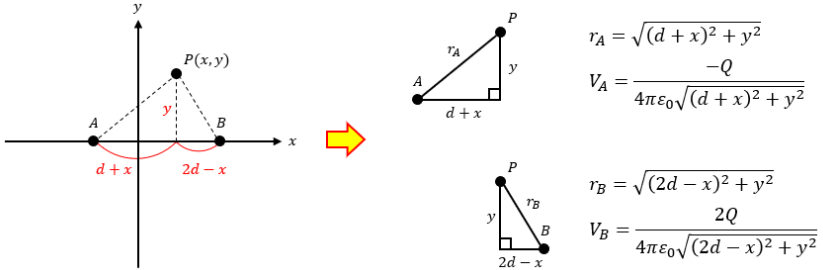
このV_AとV_Bがイコールになるので、式を整理していきます。

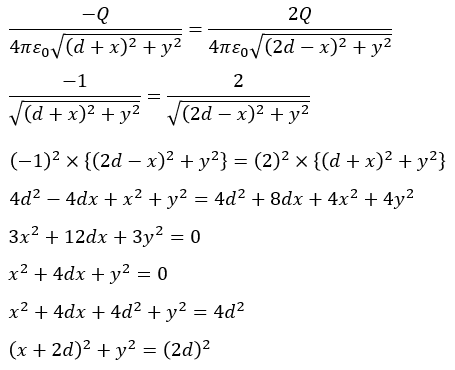
つまり、P(-2d,0)を中心とした半径2dの円が電位0[V]の等電位面となります。

以上、「2つの電荷が作る等電位面の求め方」についての説明でした。