今回は、「定電流でコンデンサを充放電した場合の挙動」についての説明です。
1.ポイント
定電流を用いているので、一次関数的に充放電が行われる。
コンデンサの充電/放電は時間経過で指数関数的に変化するというのが一般的ですよね。
ただ、例外もあります。
それが、電流源を用いた場合です。
そんな状況に遭遇する場面があるかというと謎ですけど、一応知識としてどうなるものなのかを今回はまとめてみました。
2.定電流でコンデンサを充電した場合の挙動
図1のように単純なR-C回路に電流源が繋がっているとします。
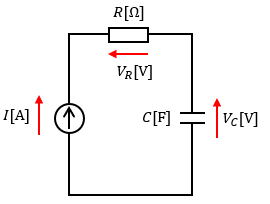
この時のコンデンサの端子電圧VC及び電源電圧Eを求めてみます。
初期条件として、t=0[s]の時のコンデンサの電荷は0[C]だとします。
単位時間当たりの電荷の変化量が電流なので、I=dQ/dtです。
ここにQ=CVの関係を適用すると、I=CdVC/dtになります。
この式を整理していきます。
t=0[s]の時はVC=0[V]、ある時間t[s]におけるコンデンサの端子電圧がVCなので、その点を考慮して積分範囲を決定します。
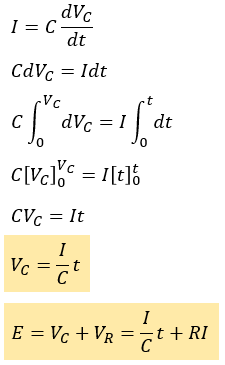
このように、電流源の場合はコンデンサの端子電圧も電源電圧も傾きI/Cで時間的変化をすることがわかります。
つまり、電圧源を使用した時のような曲線は描かず、一次関数的に充電が行われるのです。
3.定電流でコンデンサを放電した場合の挙動
図2左のようにR-C回路を形成して起電力E[V]の電源で充電し、充分に時間が経過したところで図2右のようにスイッチSを切り替えたとします。
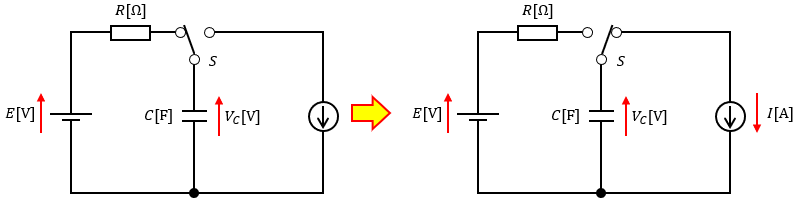
このスイッチSを切り替えた瞬間をt=0[s]とし、コンデンサはフル充電されているものとします。
この時のコンデンサの端子電圧VCを求めてみます。
基本の考え方は充電の時と変わらないですけどね。
単位時間当たりの電荷の変化量が電流なので、I=dQ/dtです。
ここにQ=CVの関係を適用すると、I=CdVC/dtになります。
この式を整理していきます。
t=0[s]の時はVC=E[V]、ある時間t[s]におけるコンデンサの端子電圧がVCなので、その点を考慮して積分範囲を決定します。
充電の時との違いはここですね。
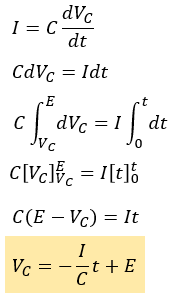
このように、電流源を用いていると、コンデンサの端子電圧の傾きが-I/Cで時間的変化をすることがわかります。
つまり、電圧源を使用した時のような曲線は描かず、一次関数的に放電が行われるのです。
充電だろうが放電だろうが、定電流だったら一次関数的になるということです。
以上、「定電流でコンデンサを充放電した場合の挙動」についての説明でした。