【基礎から学ぶコンデンサ】 2種類の誘電体が挟まれた平行板コンデンサの電束と電気力線の本数の考え方

“コンデンサ”という部品は、電気製品なら必須レベルで多用されています。
電気を蓄えたり放出したり、ノイズ成分を吸収したり、何かと便利だからです。
本記事では、そんなコンデンサという部品についての知識をわかりやすくまとめてみました。

今回は、「2種類の誘電体が挟まれた平行板コンデンサの電束と電気力線の本数の考え方」についての説明です。

１．2種類の誘電体が挟まれた平行板コンデンサの電束と電気力線の本数の考え方

図１のような同じ大きさで誘電率の異なる2種類の誘電体が挟まれている平行板コンデンサがあったとします。

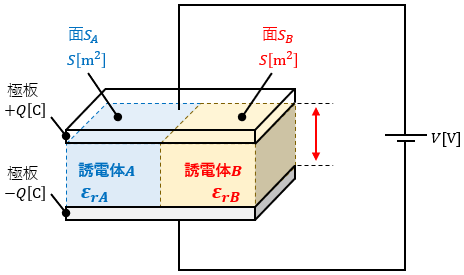
この平行板コンデンサは充電されていて、極板間電圧はE[V]、電荷はQ[C]に保たれているとします。
この時、面S_A及び面S_Bを貫く電束と電気力線の本数について考えていきたいと思います。

前提知識として電束と電気力線について理解しておく必要があるので、心配な方は先に以下の記事を参考にしてください。

まずは電束から考えてみます。

平行板コンデンサの電束密度Dは、D=εEで表されます。
平行板コンデンサの電界の強さEは、E=V/dです。
これらの式を組み合わせると、D=εV/dとなります。
なので、誘電体Aの電束密度D_Aと誘電体Bの電束密度D_Bはそれぞれ以下のようになります。

D_A=ε_rAV/d

D_B=ε_rBV/d

電束密度が求まったので、後はこれに断面積Sを掛ければ面S_A及び面S_Bを貫く電束の本数が求まります。
ということで、誘電体Aの面S_Aと誘電体Bの面S_Bを貫く電束の本数は以下のようになります。

ε_rAVS/d+ε_rBVS/d=(ε_rA+ε_rB)VS/d

ちなみに、電束の定義から、電束の総数は平行板コンデンサに蓄えられている電荷であるQ[C]になります。

次は電気力線について考えていきます。
こちらは電束と比べて単純です。

電気力線密度=電界の強さなので、誘電体Aの電界の強さE_Aと誘電体Bの電界の強さE_Bは以下のようになります。

E_A=E_B=V/d

これで電気力線密度がわかったので、断面積Sを掛けて電気力線の本数を求めると以下のようになります。

VS/d+VS/d=2VS/d

電気力線の本数に関しては誘電体に依存しないようですね。

さて、ここで違和感を覚えた人は居ますでしょうか？
電気力線の関係に以下のようなものがありました。

電気力線数N=q/ε

この関係通りだと電気力線の本数って誘電率εに依存するんですよね。
ですが、この結果を見ると誘電率には依存しなくなっています。
何故でしょうか？

答えは単純で、その関係は電荷が単位正電荷に与える力(電界の強さ)を説明する際に出てきたものだからです。
平行板コンデンサの電界の強さを考える場合、同じ考え方ではダメなのです。
現に、前者の電界の強さはE=r/4πεr²なのに対して後者の電界の強さはE=V/dと別物になっていますからね。
電気力線密度=電界の強さという関係から導き出したのがN=q/εという関係であって、この関係式は定義されたものでは無いのです。
この辺りの区別をしっかりつけていないと混乱すると思われるので注意しましょうね。

以上、「2種類の誘電体が挟まれた平行板コンデンサの電束と電気力線の本数の考え方」についての説明でした。