今回は、「対称三相交流回路の有効電力と力率の考え方」についての説明です。
1.本記事で出てくる公式や考え方のまとめページリンク
2.対称三相交流回路の有効電力と力率の考え方
「平衡三相交流回路の消費電力」でY結線回路及びΔ結線回路の消費電力について説明したので、今回は実際に問題を解きながらもう少し踏み込んだ解説をしていこうと思います。
交流回路と三相交流回路のまとめみたいな問題なので、わからない点があったら記事を都度遡って確認してみてください。
そうして何度か確認していれば勝手に記憶に定着しますので。
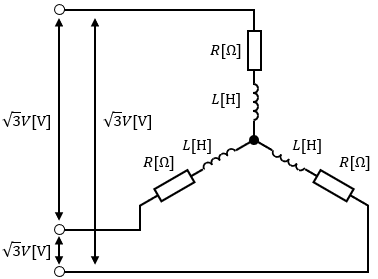
図1のような抵抗R[Ω]とインダクタンスL[H]のコイルからなる三相平衡負荷を接続したY結線に、線間電圧√3V[V]が接続されています。
角速度はω[rad/s]です。
この時の三相負荷全体の有効電力と力率がどうなるか求めてみましょう。
まず、見た目をわかりやすくするために単相ごとに回路を分けます。
線間電圧が√3Vなので、相電圧は√3V/√3=Vとなります。
つまり、単相を抜き出すとV[V]の電源に抵抗R[Ω]とインダクタンスL[H]のコイルが接続された回路と見なすことが可能です。

コイルの誘導性リアクタンスXLは角速度ω×インダクタンスLなのでωLと表せます。
ここで、以下のように抵抗Rとコイルの誘導性リアクタンスXLでインピーダンスZの直角三角形を描きます。
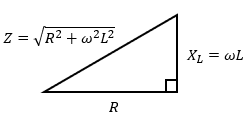
斜辺の√(R2+ω2L2)がこの回路におけるインピーダンスZです。
よって、単相回路に流れる電流Iは、I=V/√(R2+ω2L2)と表せます。
有効電力とは抵抗成分の電力のことなので、単相回路の有効電力は以下のようになります。
P=I2R=RV2/(R2+ω2L2)
後はこれが三相分になるので、3RV2/(R2+ω2L2)が三相負荷全体の有効電力です。
おさらいですが、交流回路はインピーダンスの三角形と電力の三角形を描きます。
その回路に繋がっている電圧、回路に流れる電流は抵抗成分だろうがリアクタンス成分だろうが変わらないという点は注意しましょう。
ここはちゃんと覚えておかないと混乱しやすいです。
力率はcosθのことなので、インピーダンスの三角形から求めることが可能です。
cosθ=R/Z=R/√(R2+ω2L2)
これで三相負荷全体の有効電力と力率を求めることができました。
続いて、以下のようにコンデンサのΔ結線回路を接続したら力率が1になったとします。
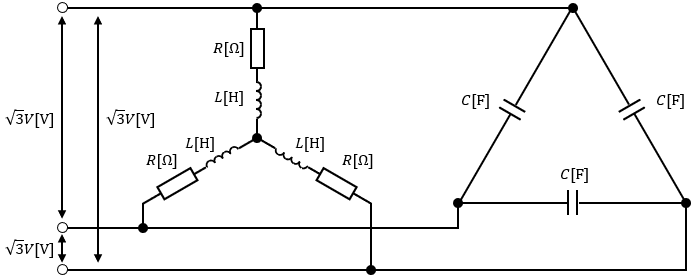
この時のコンデンサの静電容量Cを求めてみましょう。
力率が1ということは、インピーダンスにR成分しか残らなくなる…つまり、虚数部分が0になるということです。
なので、回路の合成インピーダンスを求めて、虚数部分が0になる時のCの値を求めます。
まずは単相の回路を抜き出したいのですが、この形状のままだと抜き出しが不可能です。
そこで、コンデンサのΔ結線回路をY結線回路に変換します。
平衡負荷になっている場合、Δ-Y変換をすると単相を構成するインピーダンスが1/3になったY結線になります。
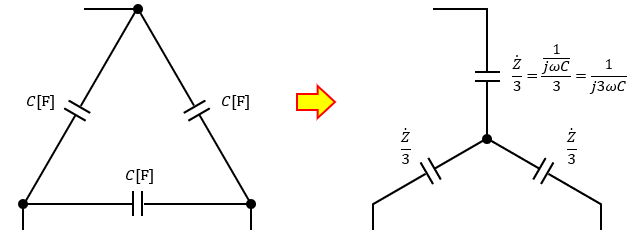
なので、単相回路を抜き出すと以下のようになります。
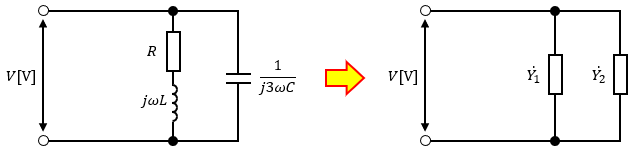
並列回路になっているので、インピーダンスではなくアドミタンスで計算していきます。
※ インピーダンスの形で和分の積にしても計算は可能。
ただ、並列の場合はアドミタンスにした方が簡単になることが多いです。
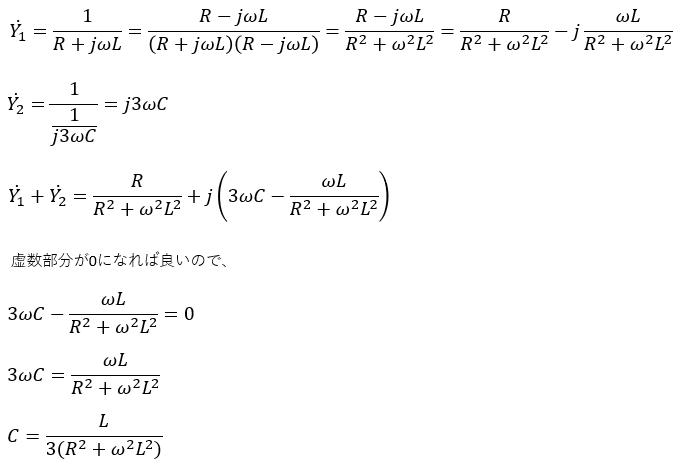
これが力率が1になる時のコンデンサの静電容量Cです。
今回の記事の内容をスラスラ解けるようになっていれば、三相交流の考え方は大体抑えられていると言えます。
以上、「対称三相交流回路の有効電力と力率の考え方」についての説明でした。





