今回は、「交流電圧の実効値の求め方(三角波編)」についての説明です。
1.ポイント
周期T[s]の交流電圧v(t)の実効値Vrmsは、以下のように定義されています。
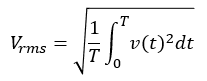
2.交流電圧の実効値の定義式
周期T[s]の交流電圧v(t)の実効値Vrmsは、以下のように定義されています。
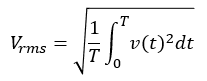
この定義式は、交流電圧を2乗して0~Tの範囲(1周期)で積分して周期Tで割ったものを平方根にしています。
つまり、2乗(Square)し、平均(Mean)し、平方根(Root)にした値になっているわけです。
このことを略してRMS(※実効値のこと)と呼ぶので、単純にその関係を式に当て嵌めたものが定義式になっているということです。
ただ、これでは何故2乗(Square)し、平均(Mean)し、平方根(Root)にすると実効値になるのかわからないですよね?
定義式を用いないで別口から実効値を求める方法は以下の記事で試しているので、気になる方はそちらも参考にしてみてください。
3.定義式を用いた三角波交流の実効値の求め方
では、定義式を使って三角波の実効値を実際に求めてみます。
図1のような振幅Vm[V]の三角波交流があります。
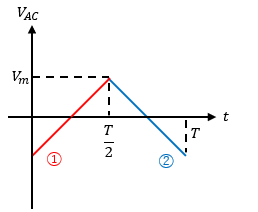
計算をしやすくするためにt=0[s]の時に-Vmになるような三角波にしていますが、気にしないでください。
この三角波を式で表すと、正弦波のように一つの式で表すことができません。
なので、部分部分で切り取って考えていく必要があります。
図1の場合、右上がりの赤線と右下がりの青線の2種類に分けて考える必要があるわけです。
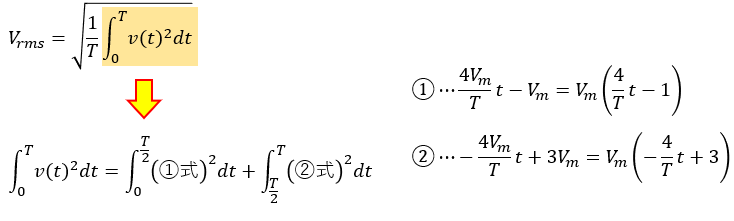
なので、別々に積分していきます。
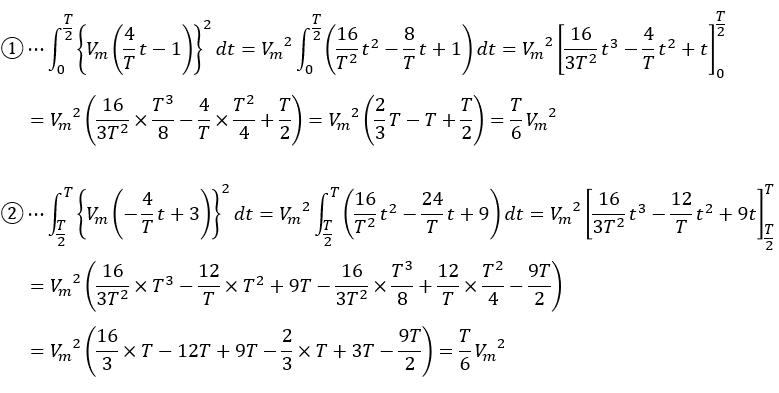
後は、定義式に代入するだけです。
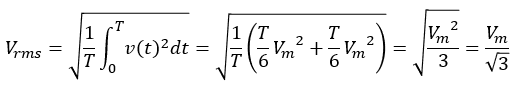
これで三角波の実効値を求めることができました。
正弦波交流の実効値と言えばVm/√2ですが、あれは交流全体の実効値ではなく、あくまで“正弦波の”実効値だという点には注意しましょうね。
以上、「交流電圧の実効値の求め方(三角波編)」についての説明でした。




