今回は、「ブリッジ回路と平衡条件」についての説明です。
1.ポイント
ブリッジ(橋渡し)している回路のこと。
ブリッジの平衡条件は、ブリッジの対辺抵抗値の積が同じになること。
つまり、R1R4=R2R3の時に平衡になる。
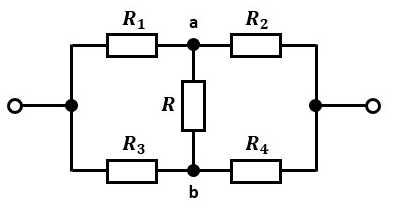
2.ブリッジ回路と平衡条件
ブリッジ回路とは図1のようなブリッジ(橋渡し)している回路のことで、図1の端子a-b間が橋渡し部に該当します。
ブリッジ回路にて抵抗値がある条件を満たしていると、a-b間の電位差が0[V]となり、a-b間の回路には電流が流れなくなる、つまり開放されているものとみなすことができます。
この状態のことを平衡状態と呼びます。
ブリッジ部分を開放すると回路が簡略化できる為、ブリッジ回路の平衡条件は知っておくと便利です。
ブリッジ回路の平衡条件は、ブリッジの対辺抵抗値の積が同じになることです。
対辺抵抗とは、ブリッジしている抵抗Rを基準にして、対角線上に位置する抵抗を指します。
つまり、R1R4=R2R3の時に平衡になります。
ブリッジブリッジ言い過ぎてブリッジがゲシュタルト崩壊しそう?しない??
平衡条件の求め方については簡単にしか触れません。
気になる方は練習だと思って計算してみましょう。
R1の両端の電圧=R3の両端の電圧、R2の両端の電圧=R4の両端の電圧になれば、a-b間の電位差は0[V]となり、a-b間の回路に電流が流れなくなるなるので、回路は平衡します。
この関係を整理するとR1R4=R2R3が導き出せます。
実際に数値を当て嵌めて、ブリッジ回路が平衡するとどうなるか見てみましょう。
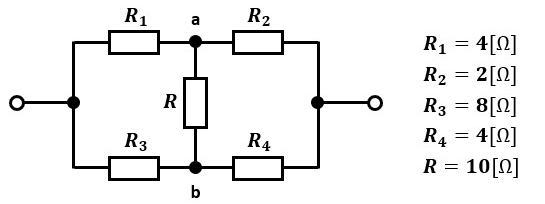
ブリッジしているので一見複雑そうに見えますが、対辺抵抗値に注目してみて下さい。
R1R4=4×4=16、R2R3=2×8=16なので、R1R4=R2R3が成り立っていますね。
つまり、このブリッジ回路は平衡しています。
その為、a-b間のブリッジ部分を開放して、図3のように置き換えることが可能です。
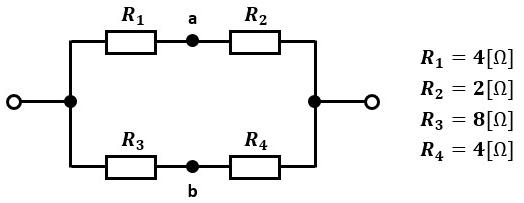
回路を簡略化できました!
ブリッジ回路に直面した場合は、平衡するか否かを最初に判断するようにすると良いですね。
以上、「ブリッジ回路と平衡条件」についての説明でした。



