今回は、「直列接続の考え方」についての説明です。
1.ポイント
2個以上の抵抗を1列に真っ直ぐ繋ぐ接続方法。
電流が一定。
直列接続時の合成抵抗は、各抵抗値の和に等しい。
電圧が抵抗値の比で比例配分される。
電車が直列接続の良い例になるかと思います。
電車って時間帯によって3両編成だったり6両編成だったりしますよね?
電車が三両編成だったとして、先頭車両をA、間の車両をB、最後尾の車両をCとすると、電車はA-B-Cの順番に一直線に・真っ直ぐに繋がりますよね?
これが直列接続のイメージです。
車両を抵抗に置き替えて考えるだけです。
数珠でも焼き鳥でも何でも良いので、真っ直ぐに繋いでいるものが直列なのです。
2.直列接続
電気回路の接続方法には、「直列接続」と「並列接続」の2つの方法があります。
今回は、「直列接続」についての説明をしていきます。
直列接続とは、2個以上の抵抗を1列に真っ直ぐ繋ぐ接続方法のことです。
なので、以下のように複数の抵抗が繋がっている状態は直列接続されていると言えます。
ちなみに、R1は1個目の抵抗、Rnはn個目の抵抗を表しています。

直列接続・並列接続に関わらず、抵抗成分は合成して1つの抵抗(合成抵抗と呼ぶ)にすることが可能です。
図1のR0が合成抵抗にあたります。
直列接続では、接続されている各抵抗値の和が合成抵抗になります。
式で表すと、以下のようになります。
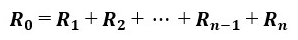
なぜ直列接続の合成抵抗が各抵抗値の和になるかと言うと、直列接続時は回路に流れる電流が一定だからです。
R1とR2が直列接続されている回路(図2上)と、R1とR2の合成抵抗であるR0で構成される回路(図2下)を比較して考えてみましょう。
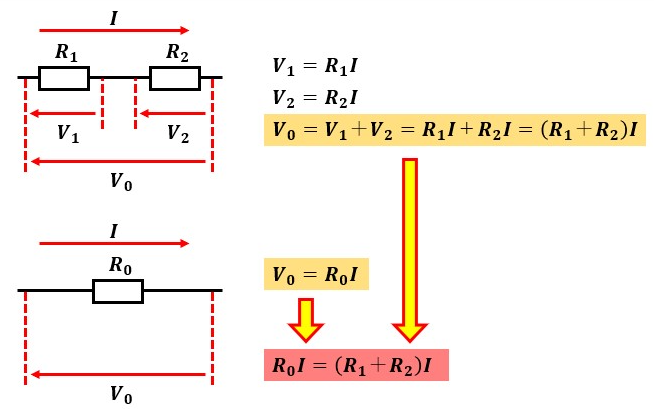
R1にかかる電圧はV1、R2にかかる電圧はV2、回路全体にかかる電圧はV0です。
図2上と図2下のそれぞれの回路には同じ起電力の電源を繋いでいるので、回路全体にかかる電圧V0は同じになると考えてください。
オームの法則から、各抵抗にかかる電圧を算出し、図2上と図2下でそれぞれV0を求めます。
計算した結果が橙塗り部分です。
図2上と図2下とでV0は同じ値になっているので、赤塗り部分が求められます。
この結果から、R0=R1+R2という関係が見出せますので、直列接続では接続されている各抵抗値の和が合成抵抗になると言えます。
直列接続時に回路に流れる電流が一定となる理由は、現時点で詳しく理解しようとすると混乱すると思いますので、簡単にまとめました。
気になる方は以下のボタンを押して下さい。
電流は電子の流れのことです。
電流1Aにつき、1秒間に通過する電子の個数は決まっています。
つまり、通過する電子の個数が変化しなければ電流も変化しません。
抵抗の中には元々電子があります。
抵抗に電子が入ってくると、入ってきた分に相当する電子を抵抗内から追い出されます。
その為、抵抗に入る前後の電子の移動個数に変化はありません。
なので、直列接続して一本道になっている経路では電子の移動個数が変化することはない=電流が一定ということになります。
また、直列接続時に回路に流れる電流が一定である為、電圧が抵抗値の比で比例配分されるという特性も出てきます。
図2にて、2つの抵抗が直列接続されている回路で、V1=R1I、V2=R2Iという関係が成り立っていました。
この2式を変形すると以下のようになります。
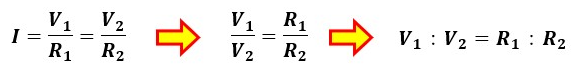
つまり、回路全体の電圧V0は、R1:R2の比で分けることができます。
これを比例配分と呼び、比例配分した各抵抗の電圧(図2のV1、V2)のことを分電圧と呼びます。
図2の分電圧を式で表すと以下のようになります。

分電圧は、全体の電圧(V0)に各抵抗値をかけて、合成抵抗で割ることで求められます。
つまり、V1を求めたいならR1、V2を求めたいならR2が分子にあたります。
ちなみに、3つ以上の抵抗を直列接続する場合も考え方は同じです。
以上、「直列接続の考え方」についての説明でした。




