今回は、「指数関数の微分」についての説明です。
1.指数関数の微分
ある点の傾きを求めることを微分と呼ぶわけですが、指数関数に対しても微分は可能です。
指数関数についてよくわかっていない方・もう忘れたという方は、以下の記事から先に読んでみてください。

【基礎から学ぶ指数対数】 そもそも指数とは何なのか? ~べき乗・累乗との関連性について~
数学は社会に出るとあまり役に立たないみたいなことを言っている人が偶にいますが、電気系の分野に進むとそうでもないです。忘れたころに中学・高校で習った内容を思い返す必要がある…ということは微妙にあります。本記事ではそんな内容の一つである“微分”について、基本からわかりやすくまとめてみました。今回はそもそも指数とは何なのかについてです。
指数関数の微分の関係式は以下の通りです。

複数ありますが、結局元となっているのは一番上の関係式ただ一つなので、今回はその式の証明をしていきます。
2.関係式の導き方
では、axを微分するとなぜaxlogeaになるのかを説明していきます。
f(x)という関数を微分する場合の定義は以下のようになっていました。
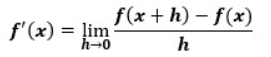
この微分の定義式に指数関数を当て嵌めて考えていきます。

ah-1=yの関係から、hを限りなく0に近づけた時、yも0に近づいていくことがわかります。
つまり、h→0にすると、y→0になります。
上記を踏まえて、axの微分をyで表します。
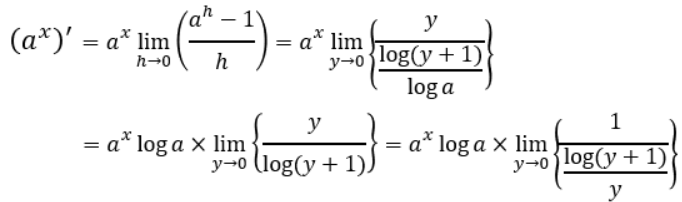
log(y+1)/yという式においてy→0にするとどうなるのかは、おそらく想像できないかと思います。
なので、ネイピア数の定義式を使って答えを導き出していきます。
ネイピア数eの定義式は、以下のようになっています。
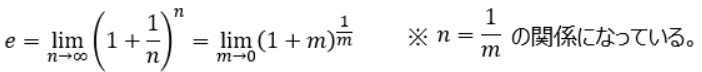
この式を両辺の自然対数(底がネイピア数eになっている対数)を取って変形していきます。
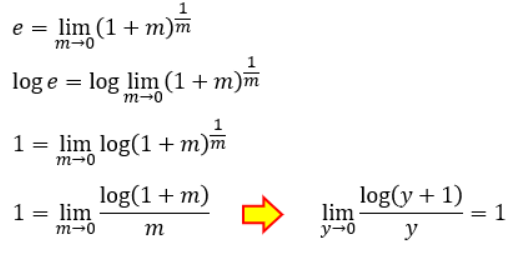
ということで、y→0の時、log(y+1)/y=1になることがわかりました。
この関係を適用することで、axを微分するaxlogeaになることがわかります。
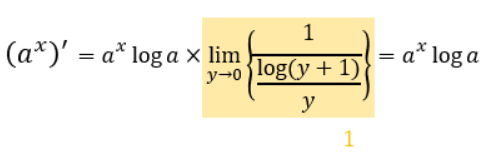
後は、この関係式から派生して残りの2式が導き出せるというわけです。
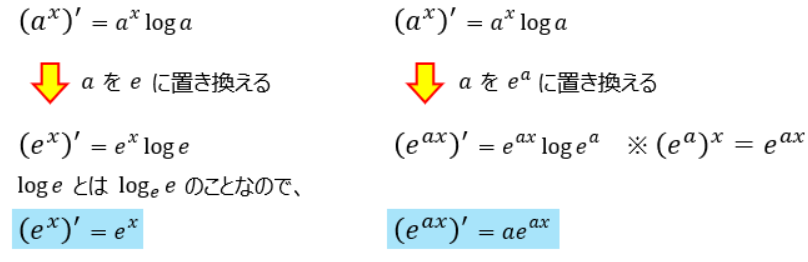
以上、「指数関数の微分」についての説明でした。




