今回は、「対数関数のグラフ表示と片対数グラフと両対数グラフの特徴」についての説明です。
目次
1.初めに
データをグラフ化する際、桁が急激に変化することは珍しくありません。
そんなデータを普通のグラフで表そうとすると、表示範囲を絞って部分的に表すか、全てが収まるスケールに目盛り設定をすることになります。
ただ、前者の場合は部分的にしか見てとれないので全体の変化の仕方が想像できませんし、後者の場合は1目盛りが大き過ぎて桁の小さな部分のデータが変化していないように見えてしまいます。
そうなると、グラフ化する意味が無いですよね?
そこで、目盛りの増え方を特殊にした対数グラフというものが登場します。
日常生活で使用する機会はまずありませんが、技術系の仕事に就くと何かと目にする機会が増えますので、知っていて損はないです。
この対数グラフには、片対数グラフ・両対数グラフという種類があります。
今回は、対数とグラフの関係について説明をしていこうと思います。
2.通常のグラフ上の対数と指数の関係
まずは、対数関数を一般的なグラフ形式で表してみます。
y=log2xという対数関数があったとします。
この関数をグラフ表示すると、以下のようになります。
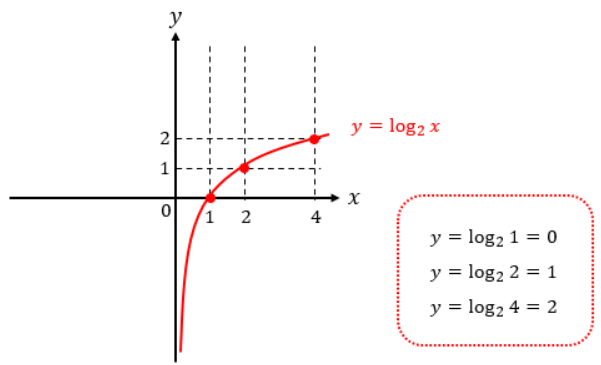
これに対して、y=2xという指数関数についても同様にプロットすると、以下のようになります。
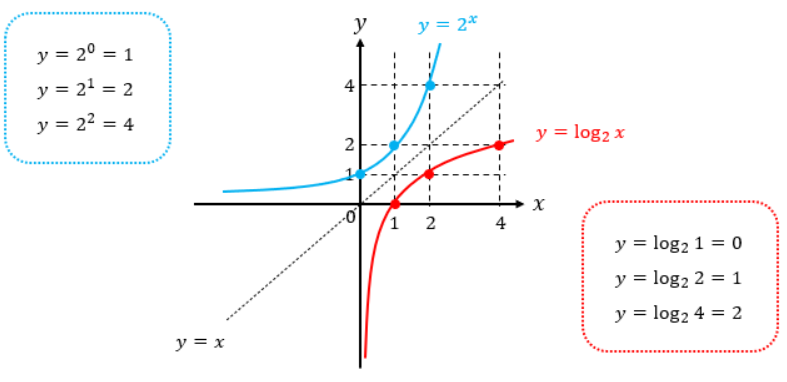
このように、対数と指数の間には「y=xを境に対称になる」という関係がありますので、覚えておきましょう。
何故こうなるのかは単純で、y=log2xを指数の形に変形するとx=2yになりますよね?
x=2yの逆数はy=2xですので、y=log2xとy=2xも逆数だとわかります。
だから対称的なグラフを描くんですね。
ちなみに、対数関数の底が0~1の間の場合、y=xの直線を跨るような変化の仕方をします。
この場合においても、関連している対数関数と指数関数のグラフはy=xを軸に対象となります。
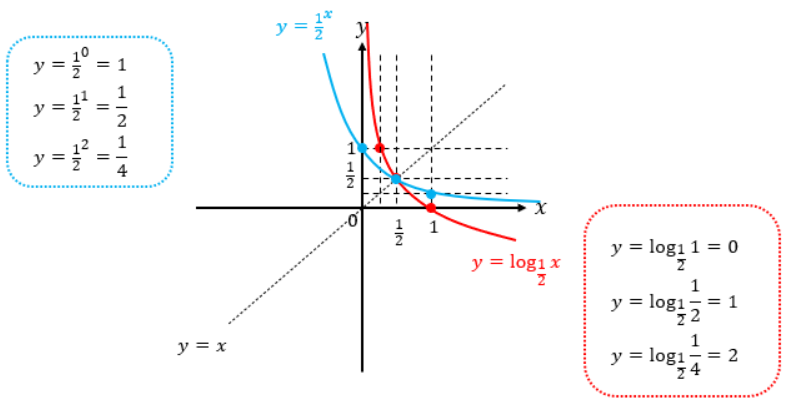
3.対数グラフの意味
対数グラフとは、簡単に言えば桁数が増えていくグラフのことです。
通常のグラフの場合、原点の次に「20」という目盛りを設けたとします。
すると、その次からの目盛りは、「40,60,80,100,120…」という具合に20ずつ数が増えていきますよね?
このように、通常のグラフは目盛りが定量的に増えていくものです。
10ずつ増えると決めたら10ずつ目盛りを刻みますし、100ずつ増えると決めたら10ずつ目盛りを刻みます。
これに対して対数グラフは、目盛りが「1,10,100,1000…」という具合に10倍されて増えていきます。
つまり、最初に述べたように桁数が増えていくんです。
このように、桁数が増えるタイプの目盛りのことを対数目盛りと呼んでいることがあります。
これが通常のグラフと対数グラフの違いです。
4.片対数グラフとは?両対数グラフとは?
では、片対数グラフと両対数グラフの違いについて説明していきます。
まあ、ここまでの説明で予想はできている人は多いと思いますが…。
- 片対数グラフ…対数グラフの中でも片方の軸のみが対数目盛りになっているタイプのグラフ。
- 両対数グラフ…対数グラフの中でも両方のが対数目盛りになっているタイプのグラフ。
以下のようなイメージです。
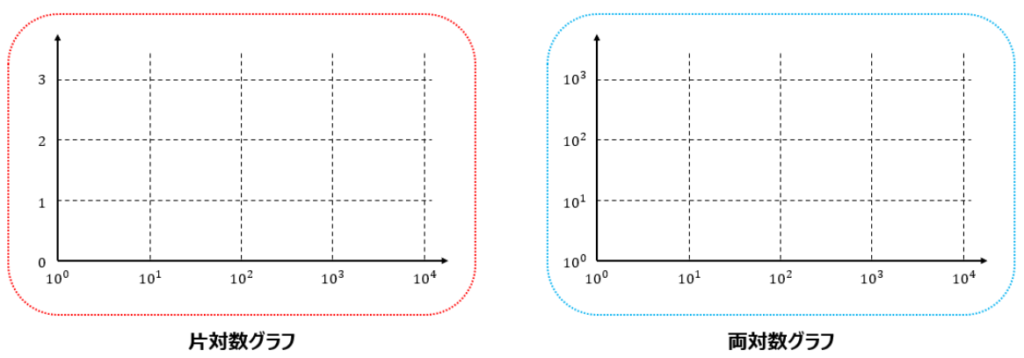
どちらを使用するかはその時にグラフ化したいデータ次第です。
x軸/y軸のどちらかだけ急激に値が変化すれば片対数グラフの方が見やすいかもしれませんし、x軸/y軸共に急激に値が変化すれば両対数グラフの方が見やすくなるかもしれません。
対数グラフは、あくまで「グラフを見やすくするための選択肢の一つ」でしかありません。
「この場合はこの形式のグラフを使用しなければならない」といったルールはありませんので、その点は勘違いしないようにしましょうね。
5.対数グラフの使用事例
どんな時に対数グラフを使用すると良いのか、例を挙げますね。
ある都道府県AとBで同じ農産物を生産していたとして、10年単位の生産量の変化が以下のようになっていたとします。
※数値は適当です。
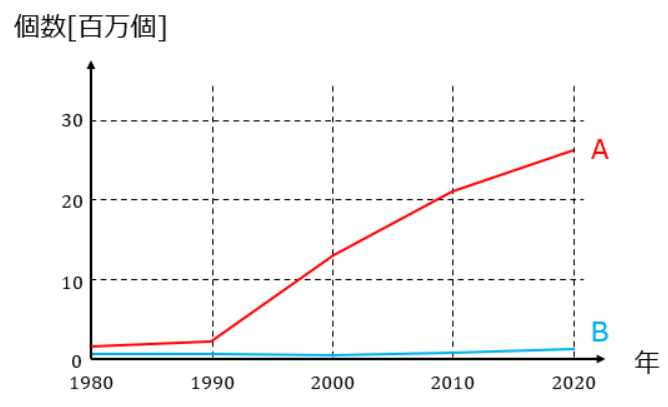
同じ農産物を生産していると言っても、Aは盛んですがBではあまり積極的には生産していないことが見てとれますね。
ただ、所々どの程度生産しているのか読み取れない箇所が存在しますよね?
こんな時に対数グラフの出番です。
生産個数が潰れて見づらいので、片対数グラフの形式にして縦軸を対数目盛りにしてみましょう。
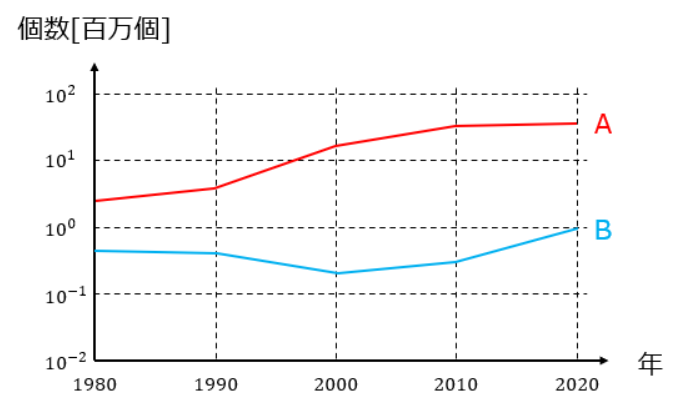
こうすると、ざっくりですがどんな程度の生産量の変化があったのか、一つのグラフから読み取れるようになるでしょう?
こんな時に対数グラフを使用するのです。
6.対数グラフの細かい目盛り
対数グラフは大体どんなものなのか説明しましたので、細かい目盛りの表現方法について記述していきます。
大まかな目盛りとしては桁が増えていくのは説明しましたが、その間についてはどう表現しているのか・どのような性質を持っているのかをまだ説明していませんからね。
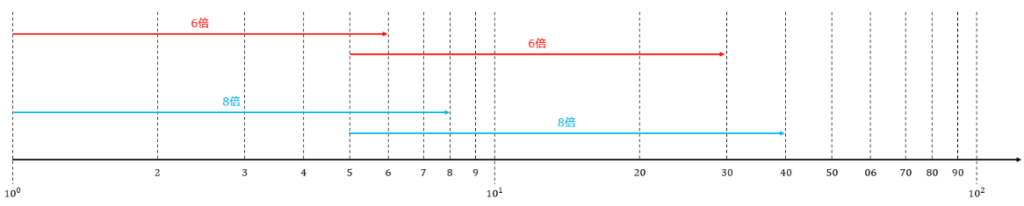
対数目盛りを細かく表すと、以下のようになります。
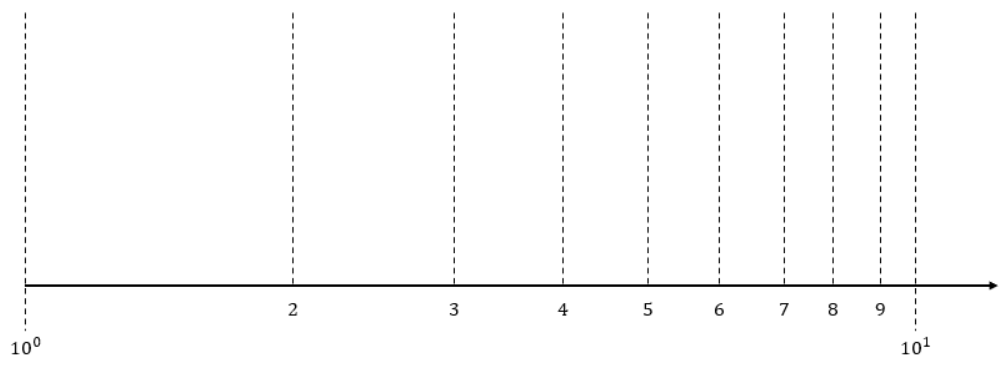
数字が大きくなるほど目盛りの間隔が狭まるんですね。
この目盛り表示の優れている点は、どの点を2倍しても同じ長さになることです。
実際その通りになっているでしょう?
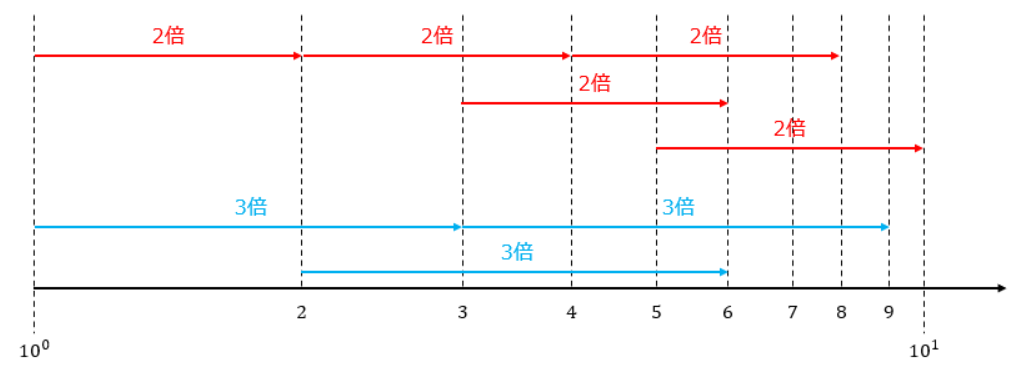
このルールをグラフ全体に適用しているのです。
7.指数と対数を対数グラフで表した時に直線になるパターン
最後に、指数と対数を対数グラフで表示しようとするとどうなるのかを記述していきます。
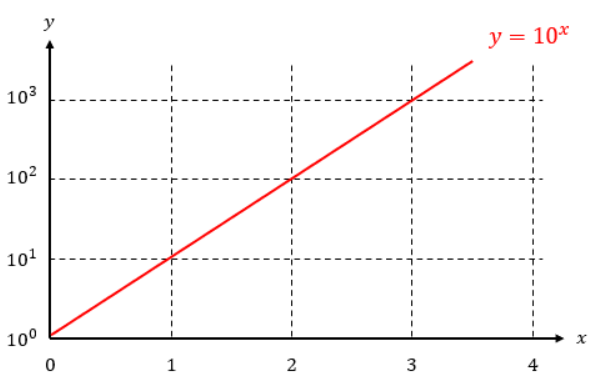
例として、y=10xという指数関数について考えます。
この指数関数は、xが定量的に増えると、yが10倍になっていきますよね?
x=1ならy=10、x=2ならy=100、x=3ならy=1000とyの値が倍々になっていきますからね。
ということは、x軸上で数値が定量的に増えると、y軸上では桁数が上がっていくと言えます。
つまり、y軸の目盛りだけ対数目盛りにした片対数グラフを使用すると、y=10xという指数関数は直線で表示できます。
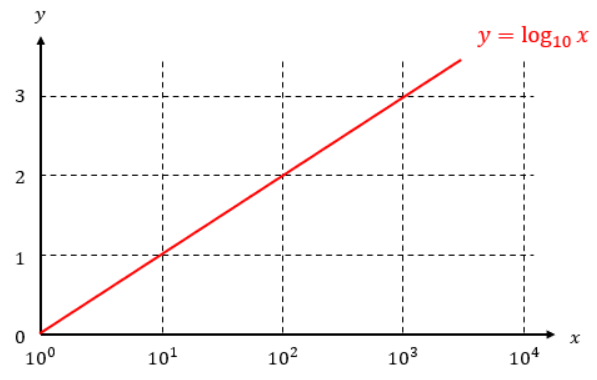
次は対数関数y=log10xについて考えていきます。
この対数関数は、先程の指数関数とは逆に、yが定量的に増えると、xが10倍になっていきます。
y=1ならx=10、y=2ならx=100、y=3ならx=1000とyの値が倍々になっていきますからね。
ということは、y軸上で数値が定量的に増えると、x軸上では桁数が上がっていくと言えます。
つまり、x軸の目盛りだけ対数目盛りにした片対数グラフを使用すると、y=log10xという対数関数は直線で表示できます。
このように、指数と対数を対数グラフで表示した場合、関係性が直線に取れるようになるパターンが存在します。
どちらの例もわかりやすいように10のn乗を使用したり底を10にしたりしましたが、別に10でなくともこの関係は適用されます。
ちなみに、よく対数グラフには「目盛りを対数で表す」という意味不明な説明がされているのですが、この説明の意味するところは上記の関係です。
確かに(x軸とy軸の)目盛り(の関係)が対数(や指数の関係)になっていますからね。
補足説明せずにそれだけ載せているサイトはもう少し読み手の気持ちを考えた方が良いと思う。
以上、「対数関数のグラフ表示と片対数グラフと両対数グラフの特徴」についての説明でした。




